题目内容
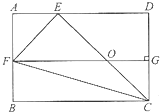 如图所示,长方形ABCD的长是12厘米,宽是8厘米,三角形CEF的面积是32平方厘米,求OG长多少厘米?
如图所示,长方形ABCD的长是12厘米,宽是8厘米,三角形CEF的面积是32平方厘米,求OG长多少厘米?分析:观察图形可知,三角形CEF被FG分成了两个以FO为底的三角形,三角形EFO的高是DG,三角形CFO的高是CG,而高DG+CG=DC=8厘米,由此利用三角形CEF的面积是32平方厘米和三角形的面积公式即可求出这两个三角形的底FO,再利用长方形的长减去FO的长度,就是OG的长度.
解答:解:
FO×DG+
FO×CG,
=
FO×(DG+CG),
=
FO×DC,
=32平方厘米;
因为DC=8厘米,
所以FO=32×2÷8=8(厘米),
则OG=12-8=4(厘米),
答:OG的长度是4厘米.
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=32平方厘米;
因为DC=8厘米,
所以FO=32×2÷8=8(厘米),
则OG=12-8=4(厘米),
答:OG的长度是4厘米.
点评:解答此题的关键是把三角形CEF看做两个以FO为底的三角形,三角形EFO的高是DG,三角形CFO的高是CG,再转化到长方形的长和宽即可解答.

练习册系列答案
相关题目
 课外拓展
课外拓展 如图所示,长方形ABCD中,AB=14厘米,AD=12厘米,现沿其对角线BD将它对折,得一几何图形,则图中阴影部分周长是
如图所示,长方形ABCD中,AB=14厘米,AD=12厘米,现沿其对角线BD将它对折,得一几何图形,则图中阴影部分周长是 如图所示,某桌球桌面为长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则 AB:BC=
如图所示,某桌球桌面为长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则 AB:BC= 如图所示,长方形ABCD中,三角形ABD的面积比三角形BCD的面积大10平方厘米,且AB=8厘米,CD=3厘米,求图中阴影部分的面积.
如图所示,长方形ABCD中,三角形ABD的面积比三角形BCD的面积大10平方厘米,且AB=8厘米,CD=3厘米,求图中阴影部分的面积. 如图所示,长方形ABCD中,AD长6cm,AB长5cm,△ADE、四边形DEBF及△CDF的面积分别相等,则△DEF的面积为
如图所示,长方形ABCD中,AD长6cm,AB长5cm,△ADE、四边形DEBF及△CDF的面积分别相等,则△DEF的面积为