题目内容
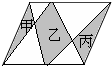如图，在平行四边形中，已知甲的面积8平方厘米，丙的面积15平方厘米，那么乙的面积是________平方厘米．
23
分析：如下图，连接EF，因为三角形ABF的面积=三角形BFE的面积（等底等高），三角形EFC的面积=三角形DFC的面积，所以乙的面积=甲的面积+丙的面积；继而得出结论．
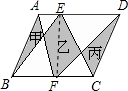
解答：连接EF，因为三角形ABF面积=三角形BFE面积（等底等高），三角形EFC面积=三角形DFC的面积，
所以乙的面积=8+15=23（平方厘米）；
答：乙的面积是23平方厘米．
故答案为：23．
点评：考查了组合图形的面积，解答此题的关键是根据三角形等底等高的性质，进行分析，把所求问题进行等量代换，进而得出结论．
分析：如下图，连接EF，因为三角形ABF的面积=三角形BFE的面积（等底等高），三角形EFC的面积=三角形DFC的面积，所以乙的面积=甲的面积+丙的面积；继而得出结论．
解答：连接EF，因为三角形ABF面积=三角形BFE面积（等底等高），三角形EFC面积=三角形DFC的面积，
所以乙的面积=8+15=23（平方厘米）；
答：乙的面积是23平方厘米．
故答案为：23．
点评：考查了组合图形的面积，解答此题的关键是根据三角形等底等高的性质，进行分析，把所求问题进行等量代换，进而得出结论．
练习册系列答案
ABC考王全优卷系列答案
相关题目
（2012?石狮市模拟）如图，在平行四边形中，甲的面积是36平方厘米，乙的面积是63平方厘米，则丙的面积是
如图，在平行四边形中，已知甲的面积8平方厘米，丙的面积15平方厘米，那么乙的面积是
如图，在平行四边形中，A、B两点是平行四边形对边上的任意两点，如果甲、乙面积分别是36cm2和30cm2，则丙的面积是
（2009?资中县）如图，在平行四边形中，甲的面积是46平方厘米，乙的面积是73平方厘米，则丙的面积是
如图，在平行四边形中，甲的面积是46平方厘米，乙的面积是73平方厘米，则丙的面积是________平方厘米．