题目内容
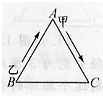 如图所示是一个边长为120m的等边三角形,甲乙同时分别从A点,B点按顺时针方向出发,甲每分钟走120m,乙每分钟走180m,但经过每个顶点时,因转弯都要耽误5s,则乙出发
如图所示是一个边长为120m的等边三角形,甲乙同时分别从A点,B点按顺时针方向出发,甲每分钟走120m,乙每分钟走180m,但经过每个顶点时,因转弯都要耽误5s,则乙出发130
130
s后第一次追上甲.分析:根据追及问题求追及时间的公式:追及时间=追及距离÷速度差,由题意得,追及的距离是120米,据此先不考虑休息时间求出乙追至上甲的时间,再加上休息时间即可.
解答:解:本题甲乙只相差一条边,则甲在休息点被追上用时最少,此时甲乙休息时间相同.
不考虑休息,乙追上甲需要:120÷(180-120)=2(分钟),
此时乙行了2×180=360米,
360÷120=3,即以正好走完3条边,
休息时间为(3-1)×5=10秒,
总用时:2×60+10=130秒.
答:乙出发130秒后第一次追上甲.
故答案为:130秒.
不考虑休息,乙追上甲需要:120÷(180-120)=2(分钟),
此时乙行了2×180=360米,
360÷120=3,即以正好走完3条边,
休息时间为(3-1)×5=10秒,
总用时:2×60+10=130秒.
答:乙出发130秒后第一次追上甲.
故答案为:130秒.
点评:此题计算关键是明白:甲在休息点被追上用时最少,根据追及时间=追及距离÷速度差,进行解答.

练习册系列答案
相关题目
 (1)量一量,如图所示正方形的边长是
(1)量一量,如图所示正方形的边长是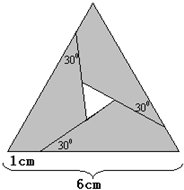 如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.
如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.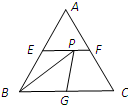 如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是
如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是 (1)量一量,如图所示正方形的边长是______厘米.
(1)量一量,如图所示正方形的边长是______厘米.