题目内容
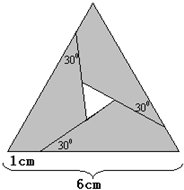 如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.
如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.问:所有斜线部分的面积是中间小等边三角形的面积的几倍?
分析:将大三角形分成边长1cm的小等边三角形即可求解.大三角形中包含36个小等边三角形,空白三角形包含3个小等边三角形.所以可得斜线部分一共有36-3=33个等边三角形,据此即可解答问题.
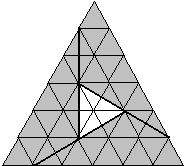

解答:解:根据题干分析可得:将大三角形分成边长1cm的小等边三角形,
观察图形可知:大三角形中包含36个小等边三角形,空白三角形包含3个小等边三角形.
所以可得斜线部分一共有36-3=33个等边三角形,
33÷3=11,
答:所有斜线部分的面积是中间小等边三角形的面积的11倍.
观察图形可知:大三角形中包含36个小等边三角形,空白三角形包含3个小等边三角形.
所以可得斜线部分一共有36-3=33个等边三角形,
33÷3=11,
答:所有斜线部分的面积是中间小等边三角形的面积的11倍.
点评:解答此题的关键是把这个大等边三角形划分出完全相同的36个小等边三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

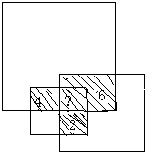 用三种不同的色纸剪成大、小、中三个正方形,把它们部分叠合地放在桌面上(如图所示),遮盖了桌面65平方厘米.如果大正方形的边长为7厘米,中正方形的边长为5厘米,小正方形的边长为3厘米,且有两层色纸遮盖的部分分别为6平方厘米,4平方厘米、2平方厘米.那么有三层色纸遮盖的部分面积为
用三种不同的色纸剪成大、小、中三个正方形,把它们部分叠合地放在桌面上(如图所示),遮盖了桌面65平方厘米.如果大正方形的边长为7厘米,中正方形的边长为5厘米,小正方形的边长为3厘米,且有两层色纸遮盖的部分分别为6平方厘米,4平方厘米、2平方厘米.那么有三层色纸遮盖的部分面积为