题目内容
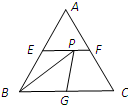如图所示，在边长为2的正三角形ABC中，E、F、G分别为AB、AC、BC的中点，点P线段EF上一个动点，连接BP、GP，则△BPG周长的最小值是3
3
．分析：连接AG交EF于M，根据等边三角形的性质证明A、G关于EF对称，得到P，△PBG周长最小，求出AB+BG即可得到答案．
解答：解：要使△PBG的周长最小，而BG=1一定，只要使BP+PG最短即可，如图：
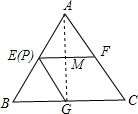
连接AG交EF于M，
因为等边△ABC，E、F、G分别为AB、AC、BC的中点，
所以AG⊥BC，EF∥BC，
则AG⊥EF，AM=MG，
A、G关于EF对称，
即当P和E重合时，此时BP+PG最小，即△PBG的周长最小，
AP=PG，BP=BE，
最小值是：PB+PG+BG=AE+BE+BG=AB+BG=2+1=3．
故答案为：3．
连接AG交EF于M，
因为等边△ABC，E、F、G分别为AB、AC、BC的中点，
所以AG⊥BC，EF∥BC，
则AG⊥EF，AM=MG，
A、G关于EF对称，
即当P和E重合时，此时BP+PG最小，即△PBG的周长最小，
AP=PG，BP=BE，
最小值是：PB+PG+BG=AE+BE+BG=AB+BG=2+1=3．
故答案为：3．
点评：本题主要考查对等边三角形的性质，轴对称-最短路线问题，平行线分线段成比例定理等知识点的理解和掌握，能求出BP+PG的最小值是解此题的关键．
练习册系列答案
相关题目
（1）量一量，如图所示正方形的边长是
如图所示，在边长为8厘米的正方形内画一条最长的圆弧．
如图所示，在边长为8厘米的正方形内画一条最长的圆弧．
（1）量一量，如图所示正方形的边长是______厘米．