题目内容
 正方形的边长为A(如图)在各边中点向顶点连线得出中间的小正方形(阴),这个小正方形的面积是
正方形的边长为A(如图)在各边中点向顶点连线得出中间的小正方形(阴),这个小正方形的面积是0.2×A×A
0.2×A×A
面积单位.分析: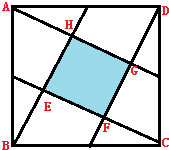
如上图所示,△ABH,△CBE,△DCF,△ADG全等,面积与中间小正方形EFGH的面积相等,可以这样证明,假设中间小正方形的边长为a,则有在△AGD中,AH=HG=a(三角形的中位线定理),同理,在△CBE中,CF=EF=a;在△ABH中BE=EH=a;
在△DCF中,DG=FG=a;S△ADG=DG×AG÷2=DG×(AH+HG)÷2=a×a,同理,S△CBE=S△DCF=S△ABH=a×a,
S?EFGH=a×a,因此大正方形被分成了五部分,而且它们的面积都相等.

如上图所示,△ABH,△CBE,△DCF,△ADG全等,面积与中间小正方形EFGH的面积相等,可以这样证明,假设中间小正方形的边长为a,则有在△AGD中,AH=HG=a(三角形的中位线定理),同理,在△CBE中,CF=EF=a;在△ABH中BE=EH=a;
在△DCF中,DG=FG=a;S△ADG=DG×AG÷2=DG×(AH+HG)÷2=a×a,同理,S△CBE=S△DCF=S△ABH=a×a,
S?EFGH=a×a,因此大正方形被分成了五部分,而且它们的面积都相等.
解答:解:假设中间小正方形的边长为a,则△ABH、△CBE、△DCF、△ADG全等且面积与中间小正方形EFGH的面积相等,
都等于a×a,大正方形被分成了五部分,而且它们的面积都相等.所以这个小正方形的面积是 五分之一的大正方形面积,即:0.2×A×A(五分之一乘A的平方).
故答案为:0.2×A×A.
都等于a×a,大正方形被分成了五部分,而且它们的面积都相等.所以这个小正方形的面积是 五分之一的大正方形面积,即:0.2×A×A(五分之一乘A的平方).
故答案为:0.2×A×A.
点评:此题考查了图形的拆拼,得出四个大三角形的面积与小正方形的面积相等,把大正方形五等分,是解决此题的关键.

练习册系列答案
相关题目
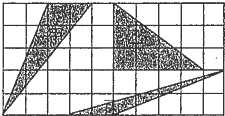 如图所示,小正方形的边长为1,三个三角形中面积最大的是( )
如图所示,小正方形的边长为1,三个三角形中面积最大的是( )
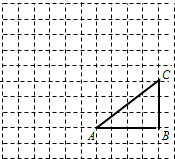 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.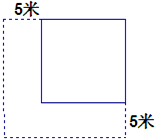 如图,一个正方形,边长增加5米,面积增加125米2,则原来这个正方形的边长为
如图,一个正方形,边长增加5米,面积增加125米2,则原来这个正方形的边长为