题目内容
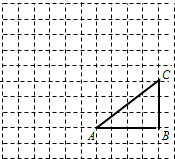 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.(1)在正方形网格中,作出△AB1C1,并用有序数对表示出B1、C1的位置;
(2)求点B旋转到B1所经过的路线长;
(3)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π)
分析:(1)让三角形的顶点B、C都绕点A逆时针旋转90°后得到对应点,顺次连接即可;再根据数对表示数的方法:第一个数表示列,第二个数表示行,写出B1、C1的位置即可.
(2)旋转过程中点B所经过的路线是一段弧,根据弧长公式计算即可.
(3)阴影部分的面积等于扇形ACC1与△ABC的面积和减去扇形ABB1与△AB1C1,而△ABC与△AB1C1的面积相等,所以阴影部分的面积等于扇形ACC1减去扇形ABB1的面积.
(2)旋转过程中点B所经过的路线是一段弧,根据弧长公式计算即可.
(3)阴影部分的面积等于扇形ACC1与△ABC的面积和减去扇形ABB1与△AB1C1,而△ABC与△AB1C1的面积相等,所以阴影部分的面积等于扇形ACC1减去扇形ABB1的面积.
解答:解:(1)如图所示:
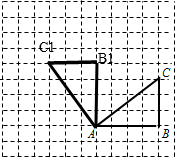
三角形AB1C1即为所求,B1的位置为:(6,6);C1的位置为:(3,6);
(2)从图中可看出这段弧的圆心角是90°,因为是直角三角形,由勾股定理得:AC=
=5,
所以点B旋转到B1所经过的路线长为:
=
;
答:点B旋转到B1所经过的路线长
π.
(3)如图所示:
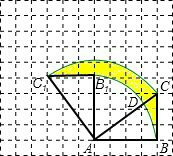 ,
,
黄色阴影部分即为旋转过程中线段BC所扫过的图形,
线段BC所扫过的图形如图所示.
根据网格图知:AB=4,BC=3,所以AC=5,
阴影部分的面积等于扇形ACC1与△ABC的面积和减去扇形ABB1与△AB1C1,
故阴影部分的面积等于扇形ACC1减去扇形ABB1的面积,两个扇形的圆心都是90度.
段BC所扫过的图形的面积S=
π(AC2-AB2)=
π×(52-42)=
π.
答:旋转过程中线段BC所扫过的图形的面积是
π.

三角形AB1C1即为所求,B1的位置为:(6,6);C1的位置为:(3,6);
(2)从图中可看出这段弧的圆心角是90°,因为是直角三角形,由勾股定理得:AC=
| 9+16 |
所以点B旋转到B1所经过的路线长为:
| 90π×5 |
| 180 |
| 5π |
| 2 |
答:点B旋转到B1所经过的路线长
| 5 |
| 2 |
(3)如图所示:
 ,
,黄色阴影部分即为旋转过程中线段BC所扫过的图形,
线段BC所扫过的图形如图所示.
根据网格图知:AB=4,BC=3,所以AC=5,
阴影部分的面积等于扇形ACC1与△ABC的面积和减去扇形ABB1与△AB1C1,
故阴影部分的面积等于扇形ACC1减去扇形ABB1的面积,两个扇形的圆心都是90度.
段BC所扫过的图形的面积S=
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
答:旋转过程中线段BC所扫过的图形的面积是
| 9 |
| 4 |
点评:(1)解决本题的关键是找出关键点.
(2)(3)本题利用了勾股定理,弧长公式、圆的面积公式求解.
(2)(3)本题利用了勾股定理,弧长公式、圆的面积公式求解.

练习册系列答案
相关题目
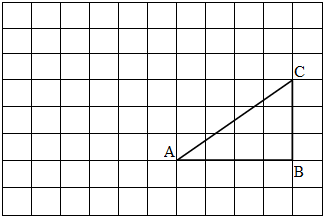
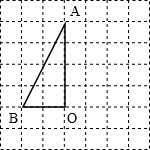 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.现把△ABO绕点O顺时针旋转90°,那么线段AO在旋转过程中所扫过的面积为( )
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.现把△ABO绕点O顺时针旋转90°,那么线段AO在旋转过程中所扫过的面积为( )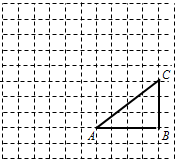 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),点B的位置表示为(10,2),点C的位置表示为(10,5),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1. 如图,正方形网格中,△ABC是格点三角形,将△ABC绕点A按逆时针方向旋转90゜得到△AB1C1.
如图,正方形网格中,△ABC是格点三角形,将△ABC绕点A按逆时针方向旋转90゜得到△AB1C1.