题目内容
 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么,按照图中所标注的数据,图中实线所围成的图形面积为________.
如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么,按照图中所标注的数据,图中实线所围成的图形面积为________.
40.5
分析:由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≌△ABG,所以AF=BG,AG=EF;同理证得△BGC≌△DHC,GC=DH,CH=BG,故FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
解答: 解:因为AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠FED=∠EFA=∠BGA=90°,
解:因为AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠FED=∠EFA=∠BGA=90°,
∠EAF+∠BAG=90°,∠ABG+∠BAG=90°?∠EAF=∠ABG,
所以AE=AB,∠EFA=∠AGB,∠EAF=∠ABG?△EFA≌△ABG,
所以AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=2+6+3+2=13,
故S= (6+3)×13-2×3-6×2=40.5.
(6+3)×13-2×3-6×2=40.5.
故答案为:40.5.
点评:本题考查的是全等三角形的判定的相关知识.作辅助线是本题的关键.
分析:由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≌△ABG,所以AF=BG,AG=EF;同理证得△BGC≌△DHC,GC=DH,CH=BG,故FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
解答:
 解:因为AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠FED=∠EFA=∠BGA=90°,
解:因为AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠FED=∠EFA=∠BGA=90°,∠EAF+∠BAG=90°,∠ABG+∠BAG=90°?∠EAF=∠ABG,
所以AE=AB,∠EFA=∠AGB,∠EAF=∠ABG?△EFA≌△ABG,
所以AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=2+6+3+2=13,
故S=
 (6+3)×13-2×3-6×2=40.5.
(6+3)×13-2×3-6×2=40.5.故答案为:40.5.
点评:本题考查的是全等三角形的判定的相关知识.作辅助线是本题的关键.

练习册系列答案
相关题目
 如图,长方形ABCD被分成两个长方形,且AB:AE=4:1,图中阴影部分三角形的面积为2平方分米.则长方形ABCD的面积为( )
如图,长方形ABCD被分成两个长方形,且AB:AE=4:1,图中阴影部分三角形的面积为2平方分米.则长方形ABCD的面积为( )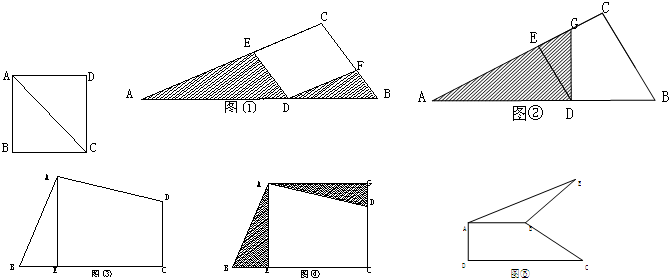
 如图,长方形ABCD被分成两个长方形,且AB:AE=4:1,图中阴影部分三角形的面积为2平方分米.则长方形ABCD的面积为
如图,长方形ABCD被分成两个长方形,且AB:AE=4:1,图中阴影部分三角形的面积为2平方分米.则长方形ABCD的面积为 平方分米
平方分米 平方分米
平方分米