题目内容
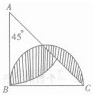 图中三角形ABC面积为12平方厘米.
图中三角形ABC面积为12平方厘米.
解:设三角形ABC的直角边为a,
由题意可得a2÷2=12,则a2=24平方厘米,
所以阴影部分的面积为:
3.14× ÷2-(12-
÷2-(12-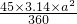 ),
),
=3.14× ÷2-(12-9.42),
÷2-(12-9.42),
=3.14×6÷2-2.58,
=9.42-2.58,
=6.84(平方厘米);
答:阴影部分的面积是6.84平方厘米.
分析:如图所示,阴影部分的面积=半圆的面积-空白①的面积,而空白①的面积=三角形ABC的面积-扇形ABD的面积,三角形的面积和扇形的圆心角已知,从而可以求解.

点评:解答此题的关键是明白:阴影部分的面积=半圆的面积-空白①的面积,而空白①的面积=三角形ABC的面积-扇形ABD的面积.
由题意可得a2÷2=12,则a2=24平方厘米,
所以阴影部分的面积为:
3.14×
 ÷2-(12-
÷2-(12-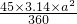 ),
),=3.14×
 ÷2-(12-9.42),
÷2-(12-9.42),=3.14×6÷2-2.58,
=9.42-2.58,
=6.84(平方厘米);
答:阴影部分的面积是6.84平方厘米.
分析:如图所示,阴影部分的面积=半圆的面积-空白①的面积,而空白①的面积=三角形ABC的面积-扇形ABD的面积,三角形的面积和扇形的圆心角已知,从而可以求解.

点评:解答此题的关键是明白:阴影部分的面积=半圆的面积-空白①的面积,而空白①的面积=三角形ABC的面积-扇形ABD的面积.

练习册系列答案
相关题目
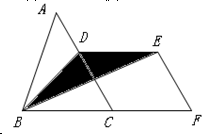 已知图中三角形ABC的面积为1998平方米,是平行四边形DEFC面积的3倍,那么图中阴影部分的面积是多少?
已知图中三角形ABC的面积为1998平方米,是平行四边形DEFC面积的3倍,那么图中阴影部分的面积是多少? 图中三角形ABC面积为12平方厘米.
图中三角形ABC面积为12平方厘米. 图中三角形ABC的面积是75cm2,把三角形ABC的边AB和AC都五等分,阴影部分的面积是
图中三角形ABC的面积是75cm2,把三角形ABC的边AB和AC都五等分,阴影部分的面积是 图中三角形ABC的面积是6平方厘米,又知C点分BE成1:2,D为EF的中点.求阴影部分的面积.
图中三角形ABC的面积是6平方厘米,又知C点分BE成1:2,D为EF的中点.求阴影部分的面积.