题目内容
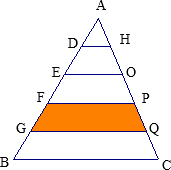
图中三角形ABC的面积是75cm2，把三角形ABC的边AB和AC都五等分，阴影部分的面积是21
21
cm2．分析：如图：根据题意，易证△AFP∽△AGQ∽△ABC，利用相似比，可求出S△AFP、S△AGQ面积比，用△AGQ的面积减去△AFP的面积就是阴影部分的面积．
解答：解：因为三角形ABC的边AB和AC都五等分，
所以△AFP∽△AGQ∽△ABC，
所以
=
，
=
，
即S△AFP：S△ABC=
，
S△AGQ：S△ABC=
，
阴影部分的面积为：S△AGQ-S△AFP=（
-
）×S△ABC，
=
×75，
=21（cm2）．
答：图中阴影部分的面积是21cm2．
故答案为：21．
所以△AFP∽△AGQ∽△ABC，
所以
| AF |
| AB |
| 3 |
| 5 |
| AG |
| AB |
| 4 |
| 5 |
即S△AFP：S△ABC=
| 9 |
| 25 |
S△AGQ：S△ABC=
| 16 |
| 25 |
阴影部分的面积为：S△AGQ-S△AFP=（
| 16 |
| 25 |
| 9 |
| 25 |
=
| 7 |
| 25 |
=21（cm2）．
答：图中阴影部分的面积是21cm2．
故答案为：21．
点评：关键是利用五等分点求得各相似三角形的相似比，再利用相似三角形的面积比等于相似比的平方的性质解决问题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图，p-ABC是一个四面体，各棱互不相等．现用红、黄两种颜色将四面染色，规则如下：
根据图中的信息解答下列问题