题目内容
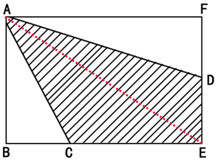
 图中三角形ABC的面积是6平方厘米,又知C点分BE成1:2,D为EF的中点.求阴影部分的面积.
图中三角形ABC的面积是6平方厘米,又知C点分BE成1:2,D为EF的中点.求阴影部分的面积.分析:如图所示,因为三角形ABC与三角形ACE等底等高,则其面积比就等于对应底的比,三角形ABC的面积已知,于是就可以求出三角形ACE的面积,也就等于知道了长方形的面积的一半的值,又因D为EF的中点,则三角形AFD的面积与三角形ADE的面积相等,且等于长方形的面积的一半的一半,据此即可求解.

解答:解:因为BC:EC=1:2,
则S△ABC:S△AEC=1:2,
又因S△ABC=6平方厘米,
所以S△AEC=6×2,
=12(平方厘米);
从而可得:S△ABE=S△AEF,
=6+12,
=18(平方厘米);
又因DF:DE=1:1,
则S△AFD=S△ADE,
=
S△AEF,
=
×18,
=9(平方厘米);
所以阴影部分的面积为:12+9=21(平方厘米);
答:阴影部分的面积是21平方厘米.
则S△ABC:S△AEC=1:2,
又因S△ABC=6平方厘米,
所以S△AEC=6×2,
=12(平方厘米);
从而可得:S△ABE=S△AEF,
=6+12,
=18(平方厘米);
又因DF:DE=1:1,
则S△AFD=S△ADE,
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=9(平方厘米);
所以阴影部分的面积为:12+9=21(平方厘米);
答:阴影部分的面积是21平方厘米.
点评:解答此题的主要依据是:等底等高的三角形的面积比等于其对应底的比.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图,p-ABC是一个四面体,各棱互不相等.现用红、黄两种颜色将四面染色,规则如下:
如图,p-ABC是一个四面体,各棱互不相等.现用红、黄两种颜色将四面染色,规则如下: 根据图中的信息解答下列问题
根据图中的信息解答下列问题