题目内容
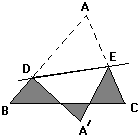 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于15
15
.分析:由题意得AE=A′E,AD=A′D,故阴影部分的周长可以转化为三角形ABC的周长.
解答:解:将△ADE沿直线DE折叠,点A落在点A′处,
所以AD=A′D,AE=A′E.
则阴影部分图形的周长等于BC+BD+CE+A′D+A′E,
=BC+BD+CE+AD+AE,
=BC+AB+AC,
=5+5+5,
=15;
答:阴影图形的周长等于15.
故答案为:15.
所以AD=A′D,AE=A′E.
则阴影部分图形的周长等于BC+BD+CE+A′D+A′E,
=BC+BD+CE+AD+AE,
=BC+AB+AC,
=5+5+5,
=15;
答:阴影图形的周长等于15.
故答案为:15.
点评:折叠问题的实质是“轴对称”,解题关键是找出经轴对称变换所得的等量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
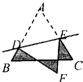 如图,等边△ABC的边长为1cm,D,E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为
如图,等边△ABC的边长为1cm,D,E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为

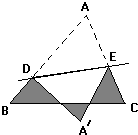 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于________.
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于________.