题目内容
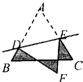 如图,等边△ABC的边长为1cm,D,E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为
如图,等边△ABC的边长为1cm,D,E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为3
3
cm.分析:由将△ADE沿直线DE折叠,点A落在点F处,根据折叠的性质,即可得AD=FD,AE=FE,又由等边三角形ABC的边长为1cm,易得阴影部分图形的周长为:BD+FD+BC+FE+EC=BD+AD+BC+AE+EC=AB+BC+AC,则可求得答案.
解答:解:因为等边三角形ABC的边长为1cm,
所以AB=BC=AC=1cm,
因为△ADE沿直线DE折叠,点A落在点F处,
所以AD=FD,AE=FE,
所以阴影部分图形的周长为:
BD+FD+BC+FE+EC
=BD+AD+BC+AE+EC
=AB+BC+AC
=1+1+1
=3(cm).
故答案为:3.
所以AB=BC=AC=1cm,
因为△ADE沿直线DE折叠,点A落在点F处,
所以AD=FD,AE=FE,
所以阴影部分图形的周长为:
BD+FD+BC+FE+EC
=BD+AD+BC+AE+EC
=AB+BC+AC
=1+1+1
=3(cm).
故答案为:3.
点评:此题考查了折叠的性质与等边三角形的性质.此题难度适中,注意掌握数形结合思想与转化思想的应用,注意掌握折叠前后图形的对应关系.

练习册系列答案
相关题目
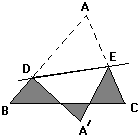 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于

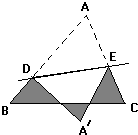 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于________.
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长等于________.