题目内容
数一数，如图中有多少个正方形？分析：首先数出单独1个小方格构成的正方形有25个，再数出由4个小方格构成的正方形有16个，再数出由9个小方格构成的正方形有9个，再数出由16个小方格构成的正方形有4个，最后数出由25个小方格构成的正方形有1个，因此问题即可解决．
解答：解：由1个小方格构成的正方形有25个，
由4个小方格构成的正方形有16个，
由9个小方格构成的正方形有9个，
由16个小方格构成的正方形有4个，
由25个小方格构成的正方形有1个，
因此图中共有 25+16+9+4+1=55个正方形．
答：一共有55个正方形．
由4个小方格构成的正方形有16个，
由9个小方格构成的正方形有9个，
由16个小方格构成的正方形有4个，
由25个小方格构成的正方形有1个，
因此图中共有 25+16+9+4+1=55个正方形．
答：一共有55个正方形．
点评：此题考查了图形的计数问题，主要利用正方性的性质，边长相等，按一定的规律数出即可．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
伯特和杰姆放学后玩智力游戏：他们用一张12×12的方格纸，依次在每个格中写有1，2，3，4…143，144这些数（如图）．如果把这些数依次相乘，比赛谁先算出积的末尾一共会有多少个连续的0？准确结果是：积的末尾一共有
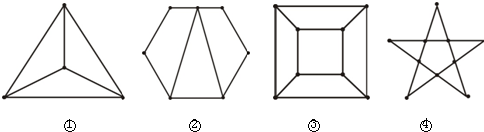
如图，①②③④四个图都称作平面图，观察图①和表中对应数值，探究计数的方法并作答．
（1）数一数，每个图各有多少个顶点，多少条边，这些边围出多少区域，并将结果填入下表：
| 图 | ① | ② | ③ | ④ |
| 顶点数m | 4 | 7 | ||
| 边数n | 6 | 9 | ||
| 区域数f | 3 |
（3）如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系，则这个平面有________条边．