题目内容
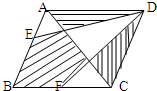 如图,ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为
如图,ABCD是平行四边形,面积为72平方厘米,E,F分别为AB,BC的中点,则图中阴影部分的面积为48
48
平方厘米.分析:如图所示,DE、DF分别于AC交于点M、N,则S△ADM=S△DMN=S△DNC,而S△AEM=S△NFC=
S△ADM,平行四边形的面积已知,则可以求出三角形ADM的面积,阴影部分的面积=平行四边形的面积-3个空白三角形的面积.
| 1 |
| 2 |
解答: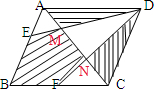 解:因为平行四边形的面积=72平方厘米,
解:因为平行四边形的面积=72平方厘米,
则S△ADC=72÷2=36(平方厘米),
S△ADM=S△DMN=S△DNC=
S△ADC=
×36=12(平方厘米),
S△AEM=S△NFC=
S△ADM=
×12=6(平方厘米),
所以阴影部分的面积=72-12-6-6,
=60-12,
=48(平方厘米);
答:阴影部分的面积是48平方厘米.
故答案为:48.
 解:因为平行四边形的面积=72平方厘米,
解:因为平行四边形的面积=72平方厘米,则S△ADC=72÷2=36(平方厘米),
S△ADM=S△DMN=S△DNC=
| 1 |
| 3 |
| 1 |
| 3 |
S△AEM=S△NFC=
| 1 |
| 2 |
| 1 |
| 2 |
所以阴影部分的面积=72-12-6-6,
=60-12,
=48(平方厘米);
答:阴影部分的面积是48平方厘米.
故答案为:48.
点评:解答此题的关键是明白:M、N是AC的三等分点,且EM:MD=FN:ND=1:2,从而逐步求解.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
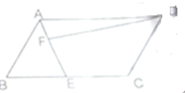 如图,ABCD是平行四边形,E是BC的中点,AF是AE的
如图,ABCD是平行四边形,E是BC的中点,AF是AE的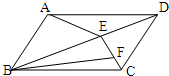 如图:ABCD是平行四边形,E是对角线BD上的一点,EF=2FC.如果三角形ABE的面积是8平方厘米,那么三角形BCF的面积是
如图:ABCD是平行四边形,E是对角线BD上的一点,EF=2FC.如果三角形ABE的面积是8平方厘米,那么三角形BCF的面积是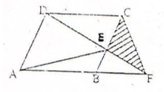 如图,ABCD是平行四边形,已知三角形ABE的面积是97平方厘米,CF长37厘米,图中阴影部分的面积是多少平方厘米?
如图,ABCD是平行四边形,已知三角形ABE的面积是97平方厘米,CF长37厘米,图中阴影部分的面积是多少平方厘米?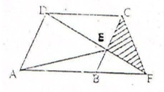 如图,ABCD是平行四边形,已知三角形ABE的面积是97平方厘米,CF长37厘米,图中阴影部分的面积是多少平方厘米?
如图,ABCD是平行四边形,已知三角形ABE的面积是97平方厘米,CF长37厘米,图中阴影部分的面积是多少平方厘米?