题目内容
 (2013?海淀区模拟)操作计算.
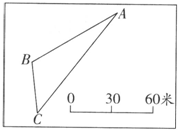
(2013?海淀区模拟)操作计算.(1)根据如图完成下列各题.
①把线段比例尺改成数值比例尺是
1:3000
1:3000
.②量得AC的长是
3
3
厘米,AC的实际长度是90
90
米.③量得∠B=
110
110
度.(精确到十位)④画出从B点到AC边的最短路线.
⑤求出△ABC的图上面积是
1.5
1.5
平方厘米.(2)自学下面这段材料,然后回答问题.
我们知道,在整数中“两个数的和等于这两个数的积”的情形并不多,例如2+2=2×2.但是在分数中,这种现象却很普遍.请观察下面的几个例子:
因为:
| 7 |
| 4 |
| 7 |
| 3 |
| 1 |
| 12 |
| 7 |
| 4 |
| 7 |
| 3 |
| 1 |
| 12 |
| 7 |
| 4 |
| 7 |
| 3 |
| 7 |
| 4 |
| 7 |
| 3 |
因为:
| 9 |
| 5 |
| 9 |
| 4 |
| 1 |
| 20 |
| 9 |
| 5 |
| 9 |
| 4 |
| 1 |
| 20 |
| 9 |
| 5 |
| 9 |
| 4 |
| 9 |
| 5 |
| 9 |
| 4 |
根据以上结果,我们发现了这样的一个规律:两个分数,如果它们的
分子
分子
相同,并且分母相差1
分母相差1
,那么这两个分数的和等于它们的积.例如| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
分析:(1)①比例尺=图上距离:实际距离,据此线段比例尺转化成数值比例尺;
②量得AC的长是3厘米,用3乘30即可求出AC的实际长度;
③用量角器量得∠B=110度;
④从B点到AC边作垂线就是从B点到AC边的最短路线;
⑤利用三角形的面积公式S=ah÷2求出三角形的面积;
(2)观察给出的式子发现:两个分数,如果它们的分子相同,并且分母相差1,那么这两个分数的和等于它们的积.例如
+
=
×
.
②量得AC的长是3厘米,用3乘30即可求出AC的实际长度;
③用量角器量得∠B=110度;
④从B点到AC边作垂线就是从B点到AC边的最短路线;
⑤利用三角形的面积公式S=ah÷2求出三角形的面积;
(2)观察给出的式子发现:两个分数,如果它们的分子相同,并且分母相差1,那么这两个分数的和等于它们的积.例如
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
解答:解:(1)1厘米:30米=1厘米:3000厘米=1:3000,
②量得AC的长是3厘米,用3×30=90(米),
③用量角器量得∠B=110度;
④从B点到AC边作垂线就是从B点到AC边的最短路线;
如图:
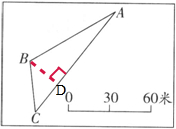
⑤AD=1厘米,
3×1÷2=1.5(平方厘米),
(2)观察给出的式子发现:两个分数,如果它们的分子相同,并且分母相差1,那么这两个分数的和等于它们的积.例如
+
=
×
.
故答案为:1:3000,3,90,110,1.5,分子,分母相差1,如
,
,
,
.
②量得AC的长是3厘米,用3×30=90(米),
③用量角器量得∠B=110度;
④从B点到AC边作垂线就是从B点到AC边的最短路线;
如图:

⑤AD=1厘米,
3×1÷2=1.5(平方厘米),
(2)观察给出的式子发现:两个分数,如果它们的分子相同,并且分母相差1,那么这两个分数的和等于它们的积.例如
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
故答案为:1:3000,3,90,110,1.5,分子,分母相差1,如
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
点评:本题主要考查了比例尺和三角形的高的作法及根据给出的式子找规律的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?海淀区模拟)右面每个小方格表示边长1厘米的正方形,画出面积是4平方厘米的三角形.
(2013?海淀区模拟)右面每个小方格表示边长1厘米的正方形,画出面积是4平方厘米的三角形.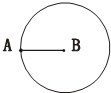 (2013?海淀区模拟)图中A、B是一个圆中的一条线段,你觉得这条线段是圆的一条半径吗?你准备如何来验证,请用你喜欢的方式表示出你的验证过程.(写出两种办法可以得满分)
(2013?海淀区模拟)图中A、B是一个圆中的一条线段,你觉得这条线段是圆的一条半径吗?你准备如何来验证,请用你喜欢的方式表示出你的验证过程.(写出两种办法可以得满分) (2013?海淀区模拟)如图,D、E分别是BC、AD的中点,如果△ABC的面积为1平方分米,则△AEC的面积是多少平方分米?(请简要写出理由)
(2013?海淀区模拟)如图,D、E分别是BC、AD的中点,如果△ABC的面积为1平方分米,则△AEC的面积是多少平方分米?(请简要写出理由)