题目内容
一个圆柱体,挖去一个最大的圆锥体,成为一个容器,这个容器的体积是原来圆柱的
- A.

- B.

- C.
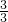
A
分析:圆柱内挖出的最大的圆锥的体积是原来圆柱的体积的 ,而这个容器的体积,就是挖去的圆锥的体积后剩下的,由此即可解答.
,而这个容器的体积,就是挖去的圆锥的体积后剩下的,由此即可解答.
解答:圆柱内最大的圆锥与原圆柱等底等高,所以圆锥的体积是原圆柱的体积的 ,
,
得到的这个容器的体积等于圆柱的体积的:1- =
= ,
,
所以这个容器的体积是原来圆柱的 .
.
故选:C.
点评:此题考查了圆柱内最大的圆锥的特点以及等底等高的圆柱与圆锥的体积倍数关系的灵活应用.
分析:圆柱内挖出的最大的圆锥的体积是原来圆柱的体积的
 ,而这个容器的体积,就是挖去的圆锥的体积后剩下的,由此即可解答.
,而这个容器的体积,就是挖去的圆锥的体积后剩下的,由此即可解答.解答:圆柱内最大的圆锥与原圆柱等底等高,所以圆锥的体积是原圆柱的体积的
 ,
,得到的这个容器的体积等于圆柱的体积的:1-
 =
= ,
,所以这个容器的体积是原来圆柱的
 .
.故选:C.
点评:此题考查了圆柱内最大的圆锥的特点以及等底等高的圆柱与圆锥的体积倍数关系的灵活应用.

练习册系列答案
相关题目
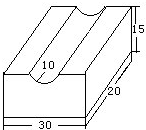 图中的几何体,是将长方体挖去一个圆柱体一半得到的,求图中几何体的体积是多少(π=3.14)?
图中的几何体,是将长方体挖去一个圆柱体一半得到的,求图中几何体的体积是多少(π=3.14)?