题目内容
9.指针停在斜线、白、黑三种区域的可能性分别是多少?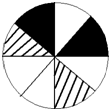
分析 总区域平均分成了8份,斜线占2份,也就是斜线的可能性是$\frac{2}{8}$,黑色也占2份,黑色的可能性是$\frac{2}{8}$,白色占4份,白色的可能性就是$\frac{4}{8}$再将分数约分成最简分数即可.
解答 解:2÷8=$\frac{1}{4}$,
2÷8=$\frac{1}{4}$,
4÷8=$\frac{1}{2}$,
答:指针停在斜线区域的可能性是$\frac{1}{4}$,指针停在黑色区域的可能性是$\frac{1}{4}$,指针停在白色区域的可能性是$\frac{1}{2}$.
点评 本题还可利用列表法或树状图法求概率(可能性),用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20.一列火车到达一站后,先下去车里人数的$\frac{1}{4}$,又上来车里人数的$\frac{1}{4}$.这时车里人数( )
| A. | 比最初少 | B. | 比最初多 | C. | 和最初一样多 |
17.一个圆柱和一个圆锥体积和高都相等,那么圆锥的底面积是圆柱底面积的( )
| A. | 2倍 | B. | 3倍 | C. | 6倍 |