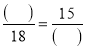题目内容
【题目】太平洋某岛国的一个部落里只有两种人：一种是永远说真话的老实人，一种是永远说假话的骗子。一天，这个部落的2009个人举行了一次圆桌会议，每个人都声称：“我左右的两个人都是骗子”。第二天，会议继续进行，但一个人因病未能到会，因此只有2008个人参加第二天的会议。大家按照新的顺序坐了下来，此时，每个人都声称：“我左右的两个人和我都不是同一种人”。参加第一天圆桌会议的人之中共有_____老实人。
【答案】670个
【解析】
第一天，由“我左右的两个人都是骗子”知，老实人的两边都是骗子，而骗子的两边至少有一个老实人，即挨着老实人的骗子的另一边可以是老实人也可以是骗子，如果挨着老实人的骗子的另一边都是骗子，则可求出老实人的最少人数；第二天，由“我左右的两个人和我都不是同一种人”，知老实人的两边都是骗子，骗子的两边至少有一个骗子，所以与老实人挨着的骗子的另一边只能是骗子，这样则“老实人、骗子、骗子”3人一组循环出现，根据老实人的最少人数乘以3，与此时的总人数作比较，进而分析求解。
将老实人用A表示，骗子用B表示，则根据第一天的排列，老实人最少的情况如图1所示，最多的情况如图2所示，从图1中可以看出，按照“ABB”循环排列，周期为3，2009÷3＝669（组）……2（人），余的2人中有一个A，即老实人最少有669＋1＝670（人）。
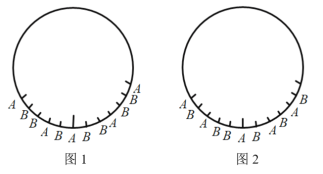
第二天，由“我左右的两个人和我都不是同一种人”，知A的两边都是B，B的两边至少有一个B，所以与A挨着的B的另一边只能是B，其排列如图3所示，从图3可以看出，按照“ABB”循环排列，由于A至少有670人，670×3＝2010（人），超出了2008，所以少的1人只能是老实人，此时老实人为669人，故第一天参加会议的老实人为670人。
故答案为：670个
