题目内容
【题目】已知圆周上任意点和直径两端点的连线形成一个角,我们把这个角称为圆周角。如图1,AB是直径,P是圆周上一点,那么∠P是圆周角。到了中学里我们会学到,圆周角总是等于90度。
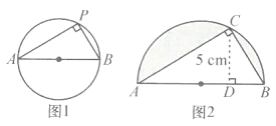
(1)图2是以AB为直径的半圆,点C是圆周上一点,CD是△ABC的高,长为5cm,已知△ABC的面积是30cm2 , 求图中阴影部分的面积。
(2)图2半圆的直径不变,当点C在半圆周上运动时,求△ABC面积的最大值。
【答案】(1)26.52 cm2
(2)36cm2
【解析】
(1)阴影部分的面积=半圆的面积-△ABC的面积,其中半圆的面积=πr2 , 半圆的直径AB=△ABC的面积×2÷CD,据此代入数据作答即可;
(2)△ABC的底AB是不变的,所以只需要高CD最大即可,因为当CD最大时,是圆的半径,所以△ABC面积的最大=AB×圆的半径×![]() 。
。
(1)AB=30×2÷5=12(cm)
S阴=(12÷2)2×3.14× ![]() -30=26.52(cm2)
-30=26.52(cm2)
(2)当△ABC面积最大值时,即高CD的长最大为半径时,
S△ABC=12×6× ![]() =36(cm2)
=36(cm2)

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
【题目】农夫将苹果树种在正方形果园里,为了保护苹果树,他在苹果树周围种了一些针叶树。下图表示了不同列数的苹果树和针叶树数量的变化情况。
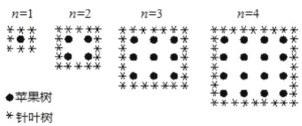
(1)完成下面的表格。
n | 苹果树数 | 针叶树数 |
8 | ||
4 | ||
5 |
(2)如果用n表示苹果树的列数,当苹果树和针叶树的棵数相等时,n的值是多少?
(3)农夫想用更多的树苗做一个更大的果园,当果园扩大时,哪一种树会增加的比较快?为什么?