题目内容
 如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)
如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)分析:如图所示,连接BO,则S△ABC-(甲+乙+丙+丁)=S阴,由题意可得:S甲=S丁,S乙=S丙(等底等高),S丙是S丁的2倍,S乙是S甲的2倍(等高不等底的三角形的面积比,等于其对应底的比),分别求出甲、乙、丙、丁的面积,即可求出阴影部分的面积.
解答:解:连接BO,则S△ABC-(甲+乙+丙+丁)=S阴,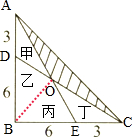
由题意可得:S甲=S丁,S乙=S丙,S丙是S丁的2倍,S乙是S甲的2倍,
三角形DBC的面积为:
6×(6+3)÷2=27(平方厘米),
S丁=S甲=27÷5=
(平方厘米),
三角形ABC的面积为:
(6+3)×(6+3)÷2=
(平方厘米),
所以阴影部分的面积为:
-(27+
),
=
-
,
=
,
=8.1(平方厘米);
答:阴影部分的面积是8.1平方厘米.

由题意可得:S甲=S丁,S乙=S丙,S丙是S丁的2倍,S乙是S甲的2倍,
三角形DBC的面积为:
6×(6+3)÷2=27(平方厘米),
S丁=S甲=27÷5=
| 27 |
| 5 |
三角形ABC的面积为:
(6+3)×(6+3)÷2=
| 81 |
| 2 |
所以阴影部分的面积为:
| 81 |
| 2 |
| 27 |
| 5 |
=
| 81 |
| 2 |
| 162 |
| 5 |
=
| 81 |
| 10 |
=8.1(平方厘米);
答:阴影部分的面积是8.1平方厘米.
点评:解答此题的主要依据是:等底等高的三角形的面积相等,等高不等底的三角形的面积比,等于其对应底的比.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2013?广州模拟)测测你的综合能力
(2013?广州模拟)测测你的综合能力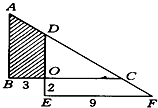 如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)
如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)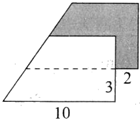 如图是由两个相同的直角梯形重叠而成的,图中只标出三个数据(单位:厘米),图中阴影部分的面积是多少平方厘米?
如图是由两个相同的直角梯形重叠而成的,图中只标出三个数据(单位:厘米),图中阴影部分的面积是多少平方厘米?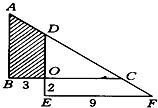 如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)
如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)