题目内容
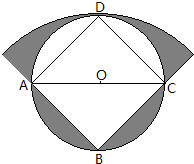图中，AC是正方形ABCD的一条对角线，且AC=8厘米，求阴影部分的面积．
解：SABCD=8×（8÷2）÷2×2，
=8×4，
=32（平方厘米）；
×π×82-32，
=×3.14×64-32，
=3.14×16-32，
=50.24-32，
=18.24（平方厘米）．
答：阴影部分的面积是18.24平方厘米．
分析：如图所示，阴影①和②和空白③和④的面积都相等，于是将阴影①、②分别移到空白③和④的位置，则阴影部分的面积=以正方形的对角线为半径的圆的面积-正方形的面积，又因正方形的对角线等于圆的直径，所以利用正方形和圆的面积公式即可求解．
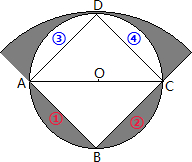
点评：解答此题的关键是明白，利用旋转和平移的方法，将阴影部分集中到一起，问题即可得解．
=8×4，
=32（平方厘米）；
×π×82-32，=
×3.14×64-32，=3.14×16-32，
=50.24-32，
=18.24（平方厘米）．
答：阴影部分的面积是18.24平方厘米．
分析：如图所示，阴影①和②和空白③和④的面积都相等，于是将阴影①、②分别移到空白③和④的位置，则阴影部分的面积=以正方形的对角线为半径的
圆的面积-正方形的面积，又因正方形的对角线等于圆的直径，所以利用正方形和圆的面积公式即可求解．点评：解答此题的关键是明白，利用旋转和平移的方法，将阴影部分集中到一起，问题即可得解．
练习册系列答案
阅读快车系列答案
相关题目
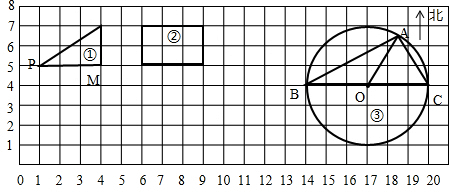
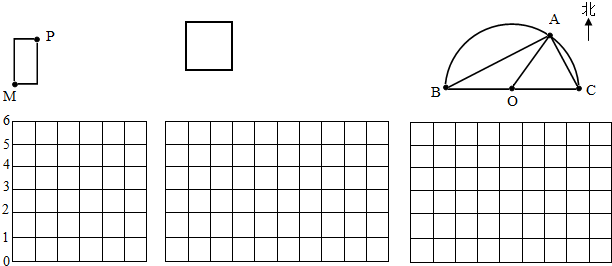
在图中画一个最大的正方形，如图所示，已知阴影部分的面积为a平方厘米，则圆的面积是（ ）平方厘米．
