题目内容
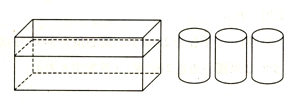
【题目】如图一个底面长30分米，宽10分米，高12分米的长方体水池，存有四分之三池水，请问：
（1）将一个高11分米，体积330立方分米的圆柱放入池中，水面的高度变为多少分米？
（2）如果再放入一个同样的圆柱，水面高度又变成了多少分米？
（3）如果再放入一个同样的圆柱，水面高度又变成了多少分米？
【答案】（1）9.9分米．（2）10.89分米．（3）12分米．
【解析】
试题分析：（1）由题意知，原来容器中的水可以看成是长30分米、宽10分米、高为12×
=9分米的长方体，现将一个高11分米，体积330立方分米的圆柱放入池中，水面没有淹没，求出圆柱的底面积即330÷11=30（平方分米）再用30×9求出淹没部分圆柱的体积除以长方体的底面积即是水升高的高度，用水升高的高度加上9分米，（2、3）同（1）解答即可．
解：（1）330÷11×12×
=30×9
=270（立方分米）
270÷（30×10）
=270÷300
=0.9（分米）
9+0.9=9.9（分米）
答：水面的高度变为9.9分米．
（2）330÷11×9.9
=30×9.9
=297（立方分米）
297÷（30×10）
=0.99（分米）
9.9+0.99=10.89（分米）
答：水面高度又变成了10.89分米．
（3）330÷11×10.89
=30×10.89
=326.7（立方分米）
326.7÷（30×10）
=1.89（分米）
10.89+1.89=12.78（分米）
有一部分水溢出，水面高度为12分米
答：水面高度又变成了12分米．
练习册系列答案
相关题目
