题目内容
【题目】观察数组(1,2,3),(3,4,5),(5,6,7),(7,8,9)的规律,求:
(1)第20组中三个数的和;
(2)前20组中所有数的和.
【答案】(1)120;(2)1260.
【解析】
试题分析:(1)观察数组发现每组是三个连续的整数,并且第几组,这组的第一个数就是几的2倍减1,据此得出第20组的三个数,再求和即可;
(2)前20组中所有数的和为6,12,18,24,30,…120也就是6×1,6×2,6×3,6×4,6×5,…,6×20,再求和即可.
解:(1)由分析知第20组数为(39,40,41),
39+40+41=120,
答:第20组中三个数的和为120;
(2)由分析知前20组中所有数的和为6×1,6×2,6×3,6×4,6×5,…,6×20,
6×1+6×2+6×3+…+6×20
=6×(1+2+3…+20)
=6×210
=1260,
答:前20组中所有数的和为1260.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
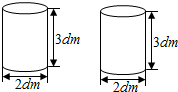 现有2根圆往形木材(如图),李师傅把其中一根加工成了一个最大的长方体,把另一根加工成了一个最大的圆锥.加工成的长方体和圆锥谁的体积大?大多少?
现有2根圆往形木材(如图),李师傅把其中一根加工成了一个最大的长方体,把另一根加工成了一个最大的圆锥.加工成的长方体和圆锥谁的体积大?大多少?