题目内容
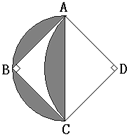 如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取3.14)
如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取3.14)
解:AC的长为2厘米,半径为1厘米,
正方形外阴影部分的面积为:3.14×12× -2×1÷2
-2×1÷2
=3.14× -1,
-1,
=1.57-1,
=0.57(平方厘米);
正方形内阴影部分的面积为:3.14×2× -2÷2
-2÷2
=6.28× -1,
-1,
=1.57-1,
=0.57(平方厘米),
0.57+0.57=1.14(平方厘米);
答:阴影部分的面积为1.14平方厘米.
分析:根据图示可知,阴影部分的面积等于正方形外阴影部分的面积加上正方形内阴影部分的面积,扇形ABC是以AC为直径的圆的面积的一半,可用以AC为直径的圆的面积的一半减去正方形面积的一半就是正方形外阴影部分的面积,正方形内阴影部分的面积等于以AD为半径的 圆的面积减去三角形ACD的面积,列式解答即可得到答案.
圆的面积减去三角形ACD的面积,列式解答即可得到答案.
点评:解答此题的关键是将阴影部分的面积分为正方形内与正方形外两部分,然后再根据圆的面积公式,正方形的面积公式进行计算即可.
正方形外阴影部分的面积为:3.14×12×
 -2×1÷2
-2×1÷2=3.14×
 -1,
-1,=1.57-1,
=0.57(平方厘米);
正方形内阴影部分的面积为:3.14×2×
 -2÷2
-2÷2=6.28×
 -1,
-1,=1.57-1,
=0.57(平方厘米),
0.57+0.57=1.14(平方厘米);
答:阴影部分的面积为1.14平方厘米.
分析:根据图示可知,阴影部分的面积等于正方形外阴影部分的面积加上正方形内阴影部分的面积,扇形ABC是以AC为直径的圆的面积的一半,可用以AC为直径的圆的面积的一半减去正方形面积的一半就是正方形外阴影部分的面积,正方形内阴影部分的面积等于以AD为半径的
 圆的面积减去三角形ACD的面积,列式解答即可得到答案.
圆的面积减去三角形ACD的面积,列式解答即可得到答案.点评:解答此题的关键是将阴影部分的面积分为正方形内与正方形外两部分,然后再根据圆的面积公式,正方形的面积公式进行计算即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形. 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?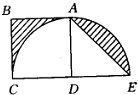 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米? 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.