题目内容
 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是20
20
平方厘米.分析:根据题意知道,阴影部分的面积等于三角形CEB的面积减去三角形CGF的面积,由此分别求出三角形CEB的面积和三角形CGF的面积即可.
解答:解:因为,△CGF∽△CBE,
所以,GC=BC×
,
GF=BE×
,
GF×GC=BC×BE×(
)2,
=10×5×
,
=10(厘米),
S(BEGF)=S△CEB-S△CGF
=
(EB×BC-CG×GF)
=
×(10×5-10)
=20(平方厘米),
答:四边形BEGF的面积等于20平方厘米,
故答案为:20.
所以,GC=BC×
| CF |
| CE |
GF=BE×
| CF |
| CE |
GF×GC=BC×BE×(
| CF |
| CE |
=10×5×
| 52 |
| 52+102 |
=10(厘米),
S(BEGF)=S△CEB-S△CGF
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=20(平方厘米),
答:四边形BEGF的面积等于20平方厘米,
故答案为:20.
点评:解答此题的关键是,知道阴影部分的面积是从哪部分面积里去掉哪部分面积,再根据相似三角形,找出边的关系,由此解答即可.

练习册系列答案
相关题目
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形. 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?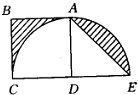 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米? 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.