题目内容
12.礼堂里一排有24个座位.小华和小明是兄弟俩,要让他俩坐在一起,并且小明坐在小华的右边.在同一排有276种不同的坐法.分析 小明坐在小华的右边,即小华坐在小明的左边,先选好小华的座位,再找出小明可以坐的位置有多少选法,然后根据加法原理解答即可.
解答 解:(1)当小华坐在最左边,小明可以坐在另外23个位子的任一个位置;
(2)当小华坐在左数第二位,小明可以坐在另外22个位子的任一个位置;
(3)当小华坐在左数第三位,小明可以坐在另外21个位子的任一个位置;
…
(23)当小华坐在左数第二十三位,小明可以坐在另外1个位子上;
那么一共有的坐法是:
23+22+21+…+2+1
=(23+1)×23÷2
=24×23÷2
=276(种).
答:在同一排有276种不同的坐法.
故答案为:276.
点评 本题考查了加法原理,关键是先确定出一个人的位置,再根据两个人的位置关系求出另一个人位置有多少种.

练习册系列答案
相关题目
17.下面的三角形是用小棒拼成的,根据图形排列的规律,第100个图形要( )根小棒.


| A. | 300 | B. | 299 | C. | 201 | D. | 240 |
4.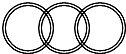 现在有若干圆环,它的外直径5厘米,环宽5毫米,将它们扣在一起,拉紧后测其长度,请你完成下列各题.
现在有若干圆环,它的外直径5厘米,环宽5毫米,将它们扣在一起,拉紧后测其长度,请你完成下列各题.
①根据表中规律,则8个环拉紧后的长度是多少厘米?
②设环的个数为a,拉紧后总长为S,你能用一个关系式表示你发现的规律吗?
③若拉紧后的长度是77厘米,它是由多少个圆环扣成的?
 现在有若干圆环,它的外直径5厘米,环宽5毫米,将它们扣在一起,拉紧后测其长度,请你完成下列各题.
现在有若干圆环,它的外直径5厘米,环宽5毫米,将它们扣在一起,拉紧后测其长度,请你完成下列各题.| 圆环个数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 拉紧后的长度(厘米) | 5 | 9 | 13 | 17 | 21 | … |
②设环的个数为a,拉紧后总长为S,你能用一个关系式表示你发现的规律吗?
③若拉紧后的长度是77厘米,它是由多少个圆环扣成的?
1.下面的等式成立是( )
| A. | $\frac{1}{3}$:$\frac{1}{2}$=3:2 | B. | 圆锥的体积=圆柱的体积×$\frac{1}{3}$ | ||
| C. | a÷b+a÷c=a÷(b+c) | D. | 直角+锐角=钝角 |