题目内容
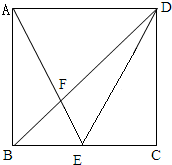 在正方形ABCD中E是BC的中点,AE与BD相交于F,三角形DEF的面积是1,那么正方形ABCD的面积是多少?
在正方形ABCD中E是BC的中点,AE与BD相交于F,三角形DEF的面积是1,那么正方形ABCD的面积是多少?
解:在正方形ABCD中,E是中点,
所以BE:AD=EF:AF=1:2,
所以三角形DEF的面积:三角形ADF的面积=1:2,又因为三角形ADF的面积是1,
所以三角形ADF的面积是1×2=2,
则三角形AED的面积是1+2=3,
所以正方形ABCD的面积是3×2=6,
答:这个正方形的面积是6.
分析:因为E是中点,那么在正方形ABCD中,根据平行线分线段成比例的性质可得:BE:AD=EF:AF=1:2,由此利用高一定时,三角形的面积与底成正比的性质求出三角形ADF的面积是1×2=2,则三角形AED的面积是1+2=3,由此即可求得正方形ABCD的面积.
点评:此题考查了平行线分线段成比例性质和高一定时,三角形面积与底成正比的性质的灵活应用.
所以BE:AD=EF:AF=1:2,
所以三角形DEF的面积:三角形ADF的面积=1:2,又因为三角形ADF的面积是1,
所以三角形ADF的面积是1×2=2,
则三角形AED的面积是1+2=3,
所以正方形ABCD的面积是3×2=6,
答:这个正方形的面积是6.
分析:因为E是中点,那么在正方形ABCD中,根据平行线分线段成比例的性质可得:BE:AD=EF:AF=1:2,由此利用高一定时,三角形的面积与底成正比的性质求出三角形ADF的面积是1×2=2,则三角形AED的面积是1+2=3,由此即可求得正方形ABCD的面积.
点评:此题考查了平行线分线段成比例性质和高一定时,三角形面积与底成正比的性质的灵活应用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 (2011?长春模拟)在正方形ABCD中E是BC的中点,AE与BD相交于F,三角形DEF的面积是1,那么正方形ABCD的面积是多少?
(2011?长春模拟)在正方形ABCD中E是BC的中点,AE与BD相交于F,三角形DEF的面积是1,那么正方形ABCD的面积是多少? 如图,在正方形ABCD中,点E是BC上的一定点,且BE=5,EC=7.点P是BD上一动点,则PE+PC的最小值是
如图,在正方形ABCD中,点E是BC上的一定点,且BE=5,EC=7.点P是BD上一动点,则PE+PC的最小值是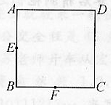 如图,在正方形ABCD中,E,F分别是边AB,BC的中点.那么,以这6个点中的任意三个为顶点可组成的不同的三角形的个数是
如图,在正方形ABCD中,E,F分别是边AB,BC的中点.那么,以这6个点中的任意三个为顶点可组成的不同的三角形的个数是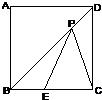 如图,在正方形ABCD中,点E是BC上的一定点,且BE=5,EC=7.点P是BD上一动点,则PE+PC的最小值是________.
如图,在正方形ABCD中,点E是BC上的一定点,且BE=5,EC=7.点P是BD上一动点,则PE+PC的最小值是________.