题目内容
14.粮仓有一批大米,第一次运走了60吨;第二次运走了余下的一半,这时余下的大米相当运走的$\frac{2}{3}$,这批大米一共有多少吨.分析 设这批大米有x吨,运走第一次后就剩余x-60吨,第二次就运走了(x-60)×$\frac{1}{2}$吨,两次就运走了x-60+(x-60)×$\frac{1}{2}$,余下的重量应该是[x-60+(x-60)×$\frac{1}{2}$]×$\frac{2}{3}$,依据运走重量+剩余重量=总重量可列方程:x-60+(x-60)×$\frac{1}{2}$+[x-60+(x-60)×$\frac{1}{2}$]×$\frac{2}{3}$=x,依据等式的性质即可求解.
解答 解:设这批大米有x吨
x-60+(x-60)×$\frac{1}{2}$+[x-60+(x-60)×$\frac{1}{2}$]×$\frac{2}{3}$=x
x-60+$\frac{1}{2}$x-30+[x-60+$\frac{1}{2}$x-30]×$\frac{2}{3}$=x
$\frac{3}{2}$x-90+[$\frac{3}{2}$x-90]×$\frac{2}{3}$=x
$\frac{3}{2}$x-90+x-60=x
$\frac{5}{2}$x-150+150=x+150
$\frac{5}{2}$-x=x+150-x
$\frac{3}{2}$x$÷\frac{3}{2}$=150$÷\frac{3}{2}$
x=100
答:这批大米一共有100吨.
点评 解答本题用方程比较容易理解,只要明确数量间的等量关系,再根据它们之间的关系列出方程即可求解.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案
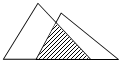 如图:阴影部分面积占大三角形面积的$\frac{2}{5}$,占小三角形面积的$\frac{1}{2}$,大三角形空白部分与小三角形空白部分面积比是3:2.
如图:阴影部分面积占大三角形面积的$\frac{2}{5}$,占小三角形面积的$\frac{1}{2}$,大三角形空白部分与小三角形空白部分面积比是3:2.