题目内容
 如图,三个圆的半径分别为1厘米、2厘米、3厘米,AB和CD垂直且过这三个圆的共有圆心O,图中阴影部分面积与非阴影部分面积之比是________.
如图,三个圆的半径分别为1厘米、2厘米、3厘米,AB和CD垂直且过这三个圆的共有圆心O,图中阴影部分面积与非阴影部分面积之比是________.
11:7
分析:由图意可知:阴影部分的面积=大圆环的面积的 +小圆环的面积的
+小圆环的面积的 +最小圆面积的
+最小圆面积的 ,进而求出空白部分的面积,再据比的意义即可得解.
,进而求出空白部分的面积,再据比的意义即可得解.
解答:阴影部分的面积为:
π×[ ×(32-22)+
×(32-22)+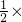 (22-12)+
(22-12)+ ×12],
×12],
=π×( +
+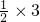 +
+ ),
),
=π×( ),
),
=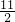 π(平方厘米),
π(平方厘米),
非阴影部分的面积为:
π×32-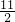 π,
π,
=9π-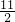 π,
π,
= π(平方厘米);
π(平方厘米);
阴影部分面积与非阴影部分面积之比是:
 :
: =11:7;
=11:7;
答:阴影部分面积与非阴影部分面积之比是11:7.
故答案为:11:7.
点评:解答此题的关键是弄清楚:阴影部分可以组合成哪些规则的图形,再据规则图形的面积和或差求解.
分析:由图意可知:阴影部分的面积=大圆环的面积的
 +小圆环的面积的
+小圆环的面积的 +最小圆面积的
+最小圆面积的 ,进而求出空白部分的面积,再据比的意义即可得解.
,进而求出空白部分的面积,再据比的意义即可得解.解答:阴影部分的面积为:
π×[
 ×(32-22)+
×(32-22)+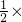 (22-12)+
(22-12)+ ×12],
×12],=π×(
 +
+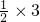 +
+ ),
),=π×(
 ),
),=
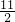 π(平方厘米),
π(平方厘米),非阴影部分的面积为:
π×32-
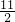 π,
π,=9π-
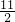 π,
π,=
 π(平方厘米);
π(平方厘米);阴影部分面积与非阴影部分面积之比是:
 :
: =11:7;
=11:7;答:阴影部分面积与非阴影部分面积之比是11:7.
故答案为:11:7.
点评:解答此题的关键是弄清楚:阴影部分可以组合成哪些规则的图形,再据规则图形的面积和或差求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图中,三个圆的半径分别是1厘米、2厘米、3厘米,图中阴影部分与空白部分的面积比是
如图中,三个圆的半径分别是1厘米、2厘米、3厘米,图中阴影部分与空白部分的面积比是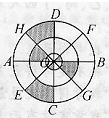 如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是
如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是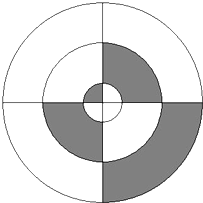
 如图中,三个圆的半径分别是1厘米、2厘米、3厘米,图中阴影部分与空白部分的面积比是________.
如图中,三个圆的半径分别是1厘米、2厘米、3厘米,图中阴影部分与空白部分的面积比是________.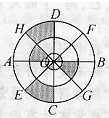 如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是________.
如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是________.