题目内容
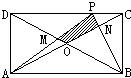 (2012?武汉模拟)如图所示,矩形ABCD的面积为24平方厘米.三角形ADM与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积是
(2012?武汉模拟)如图所示,矩形ABCD的面积为24平方厘米.三角形ADM与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积是1.8
1.8
平方厘米.分析:因三角形AOM和三角形BOC的面积相等都是长方形面积的
,可求出三角形AOM与三角形BON的面积的和,再用三角形ABP的面积减付出三角形ABO和三角形AOM和三角形BON的面积,就是四边形PMON的面积.据此解答.
| 1 |
| 4 |
解答:解:要S△AOB=24÷4=6(平方厘米),
S△AOM+S△BON
=S△AOD+S△BOC-(S△ADM+S△BCN),
=24÷4+24÷4-7.8,
=6+6-7.8,
=4.2(平方厘米),
S四边形PMON
=S△ABP-S△ABO-(S△AOM+S△BON),
=24÷2-24÷4-4.2,
=12-6-4.2,
=1.8(平方厘米).
答:四边形PMON的面积是1.8平方厘米.
故答案为:1.8.
S△AOM+S△BON
=S△AOD+S△BOC-(S△ADM+S△BCN),
=24÷4+24÷4-7.8,
=6+6-7.8,
=4.2(平方厘米),
S四边形PMON
=S△ABP-S△ABO-(S△AOM+S△BON),
=24÷2-24÷4-4.2,
=12-6-4.2,
=1.8(平方厘米).
答:四边形PMON的面积是1.8平方厘米.
故答案为:1.8.
点评:本题的关键是根据是求出S△AOM+S△BON的面积.

练习册系列答案
相关题目