题目内容
 如图,p-ABC是一个四面体,各棱互不相等.现用红、黄两种颜色将四面染色,规则如下:
如图,p-ABC是一个四面体,各棱互不相等.现用红、黄两种颜色将四面染色,规则如下:(1)首先将p,A,B,C染成红、黄二色之一;
(2)在一个面的三角形中,若两个或三个顶点同色,则将这个面染成这种颜色.
问有多少种不同的染法?(两个染好了的四面体,四个对应面的颜色相同,则认为是同-种染法,不计四个顶点的颜色是否相同)
分析:任意三点为红(或黄),PAB、PBC、ABC则四个面的都会两个点或三个点是红(或黄),所以四个面都涂成红( 或黄),有红、黄两种染法;
两点是红,如AC是红,PB是黄,则PAC和ACB是红色,其它两个面是黄色;只有两个红点两个黄点一种可能,此时必为两红面、两黄面,设底面为红,另一红面可能为三个不同侧面之一,即有三种可能;同理,底面为黄面,也有三种可能.三种情况加起来,即可得解.
两点是红,如AC是红,PB是黄,则PAC和ACB是红色,其它两个面是黄色;只有两个红点两个黄点一种可能,此时必为两红面、两黄面,设底面为红,另一红面可能为三个不同侧面之一,即有三种可能;同理,底面为黄面,也有三种可能.三种情况加起来,即可得解.
解答:解:如果有三个顶点染成同一种颜色,则不管第四点染成何色,这时四个面同色,故此时有同红或同黄两种染法.
此外,只有两个红点两个黄点一种可能,此时必为两红面、两黄面,设底面为红,另一红面可能为三个不同侧面之一,即有三种可能;
同理,底面为黄面,也有三种可能.
所以共有2+3×2=8种染法.
答:有8种不同的染法.
此外,只有两个红点两个黄点一种可能,此时必为两红面、两黄面,设底面为红,另一红面可能为三个不同侧面之一,即有三种可能;
同理,底面为黄面,也有三种可能.
所以共有2+3×2=8种染法.
答:有8种不同的染法.
点评:正确理解题意,若两个或三个顶点同色,则将这个面染成这种颜色,是解决此题的关键.

练习册系列答案
相关题目
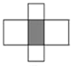 如图,阴影部分是一个长方形,它的四周是四个正方形,如果这四个正方形的周长是的和是240厘米,面积的和是1000平方厘米,那么阴影部分的面积是
如图,阴影部分是一个长方形,它的四周是四个正方形,如果这四个正方形的周长是的和是240厘米,面积的和是1000平方厘米,那么阴影部分的面积是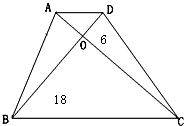 如图:四边形ABCD是一个梯形,两条对角线把梯形分成了四个小三角形,其中两个小三角形的面积分别是6平方厘米和18平方厘米.求梯形的面积.
如图:四边形ABCD是一个梯形,两条对角线把梯形分成了四个小三角形,其中两个小三角形的面积分别是6平方厘米和18平方厘米.求梯形的面积. 如图,三角形ABC是一个等腰三角形,AC=BC,已知∠ACD=130°,
如图,三角形ABC是一个等腰三角形,AC=BC,已知∠ACD=130°,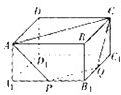 如图所示的是一个长方体,四边形APQC、是长方体的一个截面(即过长方体上4点A、P、Q、C的平面与长方体相交所得到的图形),P、Q分别为棱A1B1、B1C1,的中点,请在此长方体的平面展开图上,标出线段AC、cQ、QP、PA.
如图所示的是一个长方体,四边形APQC、是长方体的一个截面(即过长方体上4点A、P、Q、C的平面与长方体相交所得到的图形),P、Q分别为棱A1B1、B1C1,的中点,请在此长方体的平面展开图上,标出线段AC、cQ、QP、PA.