题目内容
一堆棋子有黑白两种颜色，其中黑子占
，若增加10枚白子，这时黑子占
．那么，这堆棋子有
| 7 |
| 22 |
| 2 |
| 7 |
88
88
枚．分析：本题可列方程解答，设这堆棋子共有x枚，原来黑子占
，即黑子有
x枚，若增加10枚白子，此时共有x+10枚，这时黑子占
，即有（x+10）×
枚，由此可得方程：
x=（x+10）×
．解此方程即可．
| 7 |
| 22 |
| 7 |
| 22 |
| 2 |
| 7 |
| 2 |
| 7 |
| 7 |
| 22 |
| 2 |
| 7 |
解答：解：设这堆棋子共有x枚，可得方程：
x=（x+10）×
x=
x+
，
x=
，
x=88；
答：这堆棋子共有88枚．
故答案为：88．
| 7 |
| 22 |
| 2 |
| 7 |
| 7 |
| 22 |
| 2 |
| 7 |
| 20 |
| 7 |
| 5 |
| 154 |
| 20 |
| 7 |
x=88；
答：这堆棋子共有88枚．
故答案为：88．
点评：明确这一过程中黑子数量没有发生变化，由此可列出等量关系式是完成本题的关键．
练习册系列答案
相关题目
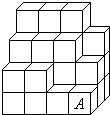14、有黑白两种颜色的正方体积木，把它摆成右图所示的形状，已知相邻的积木颜色不同，标A的为黑色，图中共有黑色积木
