题目内容
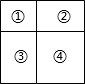
 如图,大长方形被分成了四个小长方形.已知四个小长方形的周长分别是1、2、3、4,且四个小长方形中恰有一个正方形.大长方形的面积是
如图,大长方形被分成了四个小长方形.已知四个小长方形的周长分别是1、2、3、4,且四个小长方形中恰有一个正方形.大长方形的面积是1
| 1 |
| 2 |
1
.| 1 |
| 2 |
分析:如图:首先根据正方形的周长公式:c=4a,求出小正方形①的边长,1÷4=
,长方形②的周长是2,那么它的长与宽的和是2÷2=1,则它的长为1-
=
,大长方形的宽为
+
=1;长方形④的周长是4,它的长与宽的和是4÷2=2,长方形④的长是2-
=
,那么大长方形的长为
+
=2,再根据长方形的面积公式:s=ab,据此解答.
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
| 7 |
| 4 |

解答:解:小正方形①的边长是:1÷4=
,长方形②的长与宽的和是:2÷2=1,
所以大长方形的宽是1,
长方形④的长是4÷2-(1-
)=2-
=
,
所以大长方形的长是:
+
=
,
大长方形的面积是:
×1=1
;
答:大长方形的面积是1
.
故答案为:1
.
| 1 |
| 4 |
所以大长方形的宽是1,
长方形④的长是4÷2-(1-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
所以大长方形的长是:
| 5 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
大长方形的面积是:
| 3 |
| 2 |
| 1 |
| 2 |
答:大长方形的面积是1
| 1 |
| 2 |
故答案为:1
| 1 |
| 2 |
点评:此题主要考查长方形、正方形的周长公式、面积公式的灵活运用,关键是求出大长方形的长和宽.

练习册系列答案
相关题目
 如图是一个大长方形被分成4个小长方形,其中3个小长方形的面积分别是24平方厘米,30平方厘米和32平方厘米,求阴影部分的面积.
如图是一个大长方形被分成4个小长方形,其中3个小长方形的面积分别是24平方厘米,30平方厘米和32平方厘米,求阴影部分的面积. 如图,大长方形ABCD被分成了四个小长方形,已知其 A中三个的面积(如图所示,单位:平方厘米),则大长方形 ABCD的面积是
如图,大长方形ABCD被分成了四个小长方形,已知其 A中三个的面积(如图所示,单位:平方厘米),则大长方形 ABCD的面积是 如图,大长方形被分成了四个小长方形.已知四个小长方形的周长分别是1、2、3、4,且四个小长方形中恰有一个正方形.大长方形的面积是________.
如图,大长方形被分成了四个小长方形.已知四个小长方形的周长分别是1、2、3、4,且四个小长方形中恰有一个正方形.大长方形的面积是________.