题目内容
 如图,将自然数1,2,3,…,按箭头所指方向顺序排列,依次在2,3,5,7等数的位置拐弯,如数2算做第一次拐弯处,那么第15次拐弯处的数是( )
如图,将自然数1,2,3,…,按箭头所指方向顺序排列,依次在2,3,5,7等数的位置拐弯,如数2算做第一次拐弯处,那么第15次拐弯处的数是( )分析:解这类题目最好是能找到拐弯次数n与拐弯处的数之间的关系,观察可以发现,当n 为奇数时为1+(1+3+5+…+n)=(
)2+1,据此即能求出那么第15次拐弯处的数是多少.
| n+1 |
| 2 |
解答:解:观察拐弯处的数的规律,可以得到 n个拐弯处的数,
当n 为奇数时为:1+(1+3+5+…+n)=(
)2+1,
所以第15次拐弯处的数是:(
)2+1=65.
故选:B.
当n 为奇数时为:1+(1+3+5+…+n)=(
| n+1 |
| 2 |
所以第15次拐弯处的数是:(
| 15+1 |
| 2 |
故选:B.
点评:从拐弯处数字入手,寻求它们的规律,然后灵活运用找出的规律解决问题.

练习册系列答案
相关题目
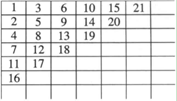 (2010?海安县)将自然数1,2,3,4…按如图那样的顺序排列起来.在最上面的一行中,从左到右第10个数是
(2010?海安县)将自然数1,2,3,4…按如图那样的顺序排列起来.在最上面的一行中,从左到右第10个数是 如图,将自然数进行排列:
如图,将自然数进行排列: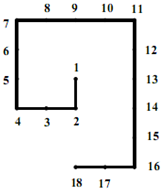 将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…
将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…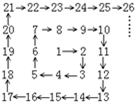 将自然数1,2,3,4…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10…等数的位置处拐弯.
将自然数1,2,3,4…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10…等数的位置处拐弯.