题目内容
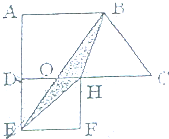 如图,直角梯形ABCD的上底和高相等,正方形DEFH的边长是6厘米,阴影部分的面积是多少平方厘米?
如图,直角梯形ABCD的上底和高相等,正方形DEFH的边长是6厘米,阴影部分的面积是多少平方厘米?从图看出:SABHD=SABE所以SBOH=SDEO于是S阴影=SDHE=
| 1 |
| 2 |
| 1 |
| 2 |
18平方厘米
18平方厘米
.分析:根据题干分析可得,△ABE和梯形ABHD的面积相等,则梯形ADOB是它们的公共部分,所以可得,△BOH和△DEO的面积相等,据此可得阴影部分的面积就等于△DEH的面积,而△DEH是正方形DEFH的一半,据此利用正方形的面积公式即可求出阴影部分的面积.
解答:解:因为SABHD=SABE,
所以SBOH=SDEO,
所以S阴影=SDHE平方厘米=
SDEFH=
×6×6=18(平方厘米),
故答案为:
SDEFH;18平方厘米.
所以SBOH=SDEO,
所以S阴影=SDHE平方厘米=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题考查了图形的等积变形在组合图形的面积计算中的灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

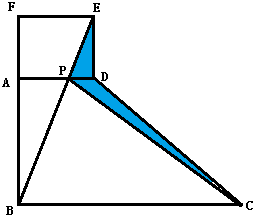 如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是( )平方厘米.
如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是( )平方厘米.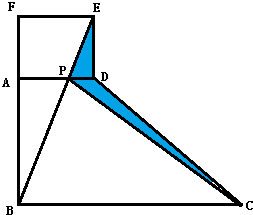 如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是平方厘米.
如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是平方厘米.