题目内容
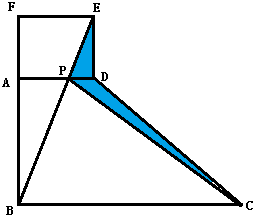如图，ABCD是个直角梯形（∠DAB=∠ABC=90°）．以AD为一边向外作长方形ADEF，其面积为6.36平方厘米，连接BE交AD于P，再连接PC．则图中阴影部分的面积是（ ）平方厘米．分析：连接AE、BD，则得到：三角形PBD的面积=三角形PCD的面积，三角形EAD的面积=三角形EBD的面积=长方形ADEF的一半，由条件长方形ADEF为6.36平方厘米可以求得结果．
解答：解：连接AE、BD，
三角形PBD的面积=三角形PCD的面积，
三角形EAD的面积=三角形EBD的面积=长方形ADEF的一半=6.36÷2=3.18（平方厘米），
故此题选B．
三角形PBD的面积=三角形PCD的面积，
三角形EAD的面积=三角形EBD的面积=长方形ADEF的一半=6.36÷2=3.18（平方厘米），
故此题选B．
点评：此题主要考查等底等高的三角形面积相等，关键是做出合适的辅助线．
练习册系列答案
相关题目
如图，ABCD是个长方形，BCFE是个正方形，AB为10厘米，BC为4厘米，P为AD边上任意一点．图中阴影部分的面积是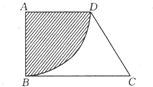
如图，ABCD是一个直角梯形，已知AD：BC=3：5，且阴影部分面积是6.28cm2，问梯形ABCD的面积是多少cm2？
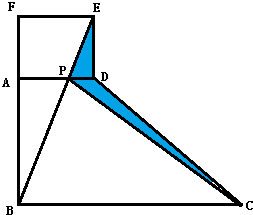如图，ABCD是个直角梯形（∠DAB=∠ABC=90°）．以AD为一边向外作长方形ADEF，其面积为6.36平方厘米，连接BE交AD于P，再连接PC．则图中阴影部分的面积是平方厘米．