题目内容
有一个三角形  ,第一次连接这个三角形三条边的中点得到
,第一次连接这个三角形三条边的中点得到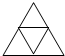 ,第2次连接中间一个三角形三条边的中点得到
,第2次连接中间一个三角形三条边的中点得到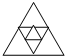 ,…依此类推.
,…依此类推.
(1)请你算出每次操作后三角形的个数填入下表.
| 操作次数 | 最初 | 第1次 | 第2次 | 第3次 |
| 三角形的个数 | 1 | 5 |
(3)要有101个三角形,应该照这样操作多少次?
解:(1)根据题干中图形可以数出第2次操作后的图形中,三角形的个数是9个,由此可以得出每增加1次操作,图形中就多出4个三角形,
即第二次操作后图形中的三角形的个数就是:1+2×4=9(个);
所以第三次操作后图形中的三角形的个数就是:1+3×4=13(个);由此可以完成下表:

(2)由(1)中的推理计算可得:当进行n次操作后图形中三角形的个数为1+4n个,
所以当n=10时,1+4×10=41(个);
答:照这样操作10次,一共有41个三角形.
(3)根据(2)中推理得出的结论可得:
设应这样操作n次,则1+4n=101,
4n=100,
n=25;
答:要有101个三角形,应该照这样操作25次.
分析:(1)首先根据所给的图形,正确数出已经给出的图形包含的三角形的个数,分别是:1,5,9;
(2)根据(1)中数的过程中,就能够发现在前一个图的基础上依次多4个.
点评:此类题找规律的时候,主要应发现前后图形中个数之间的变化和联系.
即第二次操作后图形中的三角形的个数就是:1+2×4=9(个);
所以第三次操作后图形中的三角形的个数就是:1+3×4=13(个);由此可以完成下表:

(2)由(1)中的推理计算可得:当进行n次操作后图形中三角形的个数为1+4n个,
所以当n=10时,1+4×10=41(个);
答:照这样操作10次,一共有41个三角形.
(3)根据(2)中推理得出的结论可得:
设应这样操作n次,则1+4n=101,
4n=100,
n=25;
答:要有101个三角形,应该照这样操作25次.
分析:(1)首先根据所给的图形,正确数出已经给出的图形包含的三角形的个数,分别是:1,5,9;
(2)根据(1)中数的过程中,就能够发现在前一个图的基础上依次多4个.
点评:此类题找规律的时候,主要应发现前后图形中个数之间的变化和联系.

练习册系列答案
相关题目
 如图,有一个边长为1的正三角形,第一次去掉三边中点连线围成的那个正三角形;第二次对留下的三个正三角形,再分别去掉它们中点连线围成的三角形;…做到第四次后,一共去掉了
如图,有一个边长为1的正三角形,第一次去掉三边中点连线围成的那个正三角形;第二次对留下的三个正三角形,再分别去掉它们中点连线围成的三角形;…做到第四次后,一共去掉了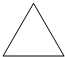 ,第一次连接这个三角形三条边的中点得到
,第一次连接这个三角形三条边的中点得到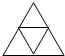 ,第2次连接中间一个三角形三条边的中点得到
,第2次连接中间一个三角形三条边的中点得到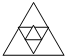 ,…依此类推.
,…依此类推.