题目内容
如图所示，两个形状和大小都相同的直角△ACB和△EDF的面积都是10cm2，每个直角的直角顶点都恰好落在另一个直角三角形斜边上，这两个直角三角形的重叠部分是一个长方形．那么四边形ABEF的面积是20
20
cm2．分析：因为重叠部分是一个长方形，所以∠1=∠3，2=∠1，可得∠2=∠3，因此AB∥EF，又因为AB=EF，所以四边形ABEF是平行四边形，那么直角△ACB和△EDF的面积都与四边形ABEF等底等高，直角△ACB和△EDF的面积都是四边形ABEF的面积的一半，那么四边形ABEF的面积是：10×2=20cm2．
解答：解：根据分析可得：直角△ACB和△EDF的面积都是四边形ABEF的面积的一半，
那么四边形ABEF的面积是：10×2=20（cm2）．
故答案为：20．
那么四边形ABEF的面积是：10×2=20（cm2）．
故答案为：20．
点评：本题关键是能够看出四边形ABEF是平行四边形，然后利用等底等高的三角形与平行四边形的面积关系解答即可．
练习册系列答案
相关题目
十个相同的圆摆成左如图所示的形状，过其中两个圆的圆心A和B作直线，求直线右上方圆内总面积与直线左下方圆内总面积的比．
仔细观察如图1所示的两个圆，并回答问题．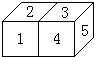
两个同样大小的正方体形状的积木．每个正方体上相对的两个面上写的数之和都等于9．现将两个正方体并列放置．看得见的五个面上的数字如图所示，则看不见的七个面上的数的和等于
（2012?佛山）华英学校计划使用如图所示尺寸的4个形状相同的长方形地砖和一个正方形地砖组成的图案铺设风雨走廊．已知走廊也为长方形，长度为18米，宽度是0.6米，长方形地转为3元/块．正方形地转为2元/块．