题目内容
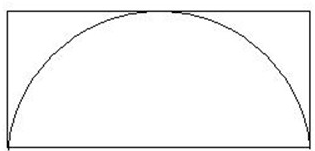
 已知如图中长方形的面积是22
已知如图中长方形的面积是22| 2 |
| 3 |
8
| 1 |
| 2 |
8
平方厘米.| 1 |
| 2 |
分析:根据题意知A、B两点分别是长方形的长和宽的中点,可知小空白三角形ABC,与大三角形CDE面积的比是1:4,即阴间部分面积是三角形CDE面积的
,三角形CDE的面积是长方形面积的一半.据此解答.
| 3 |
| 4 |
解答:解:

AC=
AE,BC=
BD,
所以:S△ABC=
S△CDE,
S四边形ABDE=
S△CDE,
S△CDE=22
÷2=11
(平方厘米),‘
S四边形ABDE=
×11
=8
(平方厘米).
答:阴影部分的面积是8
平方厘米.
故答案为:8
.

AC=
| 1 |
| 2 |
| 1 |
| 2 |
所以:S△ABC=
| 1 |
| 4 |
S四边形ABDE=
| 3 |
| 4 |
S△CDE=22
| 2 |
| 3 |
| 1 |
| 3 |
S四边形ABDE=
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
答:阴影部分的面积是8
| 1 |
| 2 |
故答案为:8
| 1 |
| 2 |
点评:本题的关键是求出阴影部分的面积是三角形CDE面积的几分之几,再进行解答.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目

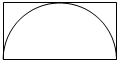 已知如图中长方形的周长是60厘米,求半圆的面积.
已知如图中长方形的周长是60厘米,求半圆的面积. 已知如图中长方形的面积是22
已知如图中长方形的面积是22 平方厘米,A、B两点分别是长方形的长和宽的中点,图中阴影部分的面积是________平方厘米.
平方厘米,A、B两点分别是长方形的长和宽的中点,图中阴影部分的面积是________平方厘米.