题目内容
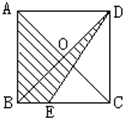如图，在正方形ABCD中EC=2BE，三角形 BOC的面积是3平方米，求阴影部分的面积．
解：阴影部分的面积是：
△ABO+△BED，
=
AB×（BC）+×（
BC）×CD，
=
AB×BC+
BC×CD，
因为AB×BC=12，BC×CD=12，
所以=×12+×12，
=5（平方米）；
答：阴影部分的面积是5平方米．
分析：在正方形ABCD中EC=2BE，也就是说BE=BC，所以E点是BC 的3等分点，△BED的底就是BC，高就是CD，△ABO的底是AB高是BC，因为△BOC的面积是3平方米，所以正方形的面积就是3×4=12平方米，也就是说正方形的边长×边长=12，由此可以解决阴影部分的面积．
点评：本题主要考查了三角形及正方形面积公式的掌握及运用情况，考查了学生灵活解决问题的能力．
△ABO+△BED，
=
AB×（BC）+×（BC）×CD，=
AB×BC+BC×CD，因为AB×BC=12，BC×CD=12，
所以=
×12+×12，=5（平方米）；
答：阴影部分的面积是5平方米．
分析：在正方形ABCD中EC=2BE，也就是说BE=
BC，所以E点是BC 的3等分点，△BED的底就是BC，高就是CD，△ABO的底是AB高是BC，因为△BOC的面积是3平方米，所以正方形的面积就是3×4=12平方米，也就是说正方形的边长×边长=12，由此可以解决阴影部分的面积．点评：本题主要考查了三角形及正方形面积公式的掌握及运用情况，考查了学生灵活解决问题的能力．
练习册系列答案
相关题目
（2012?汨罗市模拟）如图每个小正方形的边长表示1厘米．
如图，在10×10正方形网格中，每个小正方形的边长均为1个单位．将△ABC向下平移4个单位，得到△A′B′C′，再把△A′B′C′绕点C′顺时针旋转90°，得到△A″B″C″，请你画出△A′B′C′和△A″B″C″（不写画法）．
