题目内容
 如图,在平行四边形ABCD中,BE交AC于点F,交CD于点E,己知三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米.那么,四边形ADEF的面积是
如图,在平行四边形ABCD中,BE交AC于点F,交CD于点E,己知三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米.那么,四边形ADEF的面积是27.5
27.5
平方厘米.分析:因为三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米,则EF:BF=10:15=2:3,则三角形BFC的面积和三角形ABF的面积比也是2:3,于是可以求出三角形ABCF面积,进而得出三角形ADC的面积,从而求出四边形ADEF的面积.
解答:解:因为三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米,
则EF:BF=10:15=2:3,
则三角形BFC的面积和三角形ABF的面积比也是2:3,
所以三角形ABCF面积是15÷
=22.5(平方厘米),
因此三角形ADC的面积为:22.5+15=37.5(平方厘米),
所以四边形ADEF的面积是37.5-10=27.5(平方厘米);
答:四边形ADEF的面积是27.5平方厘米.
故答案为:27.5.
则EF:BF=10:15=2:3,
则三角形BFC的面积和三角形ABF的面积比也是2:3,
所以三角形ABCF面积是15÷
| 2 |
| 3 |
因此三角形ADC的面积为:22.5+15=37.5(平方厘米),
所以四边形ADEF的面积是37.5-10=27.5(平方厘米);
答:四边形ADEF的面积是27.5平方厘米.
故答案为:27.5.
点评:解答此题的主要依据是:等高不等底的三角形的面积比等于其对应底的比,等底等高的三角形面积相等.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (1)在如图所示方格中画一个直角三角形,其中两个顶点位置分别是A(3,7)和B(1,4),你所画的第三个顶点C位置是( 3,
(1)在如图所示方格中画一个直角三角形,其中两个顶点位置分别是A(3,7)和B(1,4),你所画的第三个顶点C位置是( 3, 如图,在平行四边形中,A、B两点是平行四边形对边上的任意两点,如果甲、乙面积分别是36cm2和30cm2,则丙的面积是
如图,在平行四边形中,A、B两点是平行四边形对边上的任意两点,如果甲、乙面积分别是36cm2和30cm2,则丙的面积是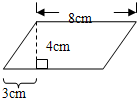 (2010?保靖县)如图,把平行四边形沿高剪开,在把三角形向右平移( )cm,可以得到一个与原图形面积相等的长方形.
(2010?保靖县)如图,把平行四边形沿高剪开,在把三角形向右平移( )cm,可以得到一个与原图形面积相等的长方形.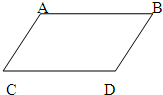 如图是一个平行四边形,(1)过A点画对边CD的垂线,(2)再过D点画对边AB的垂线,(3)在AB上任取一点,画CD的垂线,(4)你发现了什么?
如图是一个平行四边形,(1)过A点画对边CD的垂线,(2)再过D点画对边AB的垂线,(3)在AB上任取一点,画CD的垂线,(4)你发现了什么?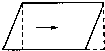 如图,在推导平行四边形面积时,通过平移,把平行四边形转变为长方形.长方形与平行四边形相比( )
如图,在推导平行四边形面积时,通过平移,把平行四边形转变为长方形.长方形与平行四边形相比( )