题目内容
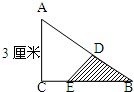 直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.
直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.
解:如图,

△ABC的面积:3×4÷2=6(平方厘米)
由折叠可知,△ACE的面积等于△ADE的面积,AD=AC=3厘米,BD=5-3=2(厘米)
因为△ADE和△BDE等高,AD:BD=3:2,因此,△ADE的面积:△BDE的面积=3:2
又因为ACE的面积等于△ADE的面积,
所以△BDE的面积是△ABC面积的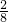 ,即
,即
所以阴影部分的面积是6× =1.5(平方厘米)
=1.5(平方厘米)
答:阴影部分的面积是1.5平方厘米;
故答案为:1.5平方厘米
分析:如图,由折叠可知,△ACE的面积等于△ADE的面积,AD=AC=3厘米,BD=5-3=2(厘米),由于△ADE和△BDE等高,AD:BD=3:2,因此,△ADE的面积:△BDE的面积=3:2,又由于,△ACE的面积等于△ADE的面积,△BDE的面积是△ABC面积的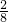 ,即
,即 ,△ABC的面积由题中提供数据即可求出,进而即可求出阴影部分(△BDE)面积.
,△ABC的面积由题中提供数据即可求出,进而即可求出阴影部分(△BDE)面积.
点评:本题是考查图形的折叠问题、三角形面积的计算是等,此种解答方法的关键是理解△BDE的面积是△ABC面积的 .此题还可用相似三角形解答.
.此题还可用相似三角形解答.

△ABC的面积:3×4÷2=6(平方厘米)
由折叠可知,△ACE的面积等于△ADE的面积,AD=AC=3厘米,BD=5-3=2(厘米)
因为△ADE和△BDE等高,AD:BD=3:2,因此,△ADE的面积:△BDE的面积=3:2
又因为ACE的面积等于△ADE的面积,
所以△BDE的面积是△ABC面积的
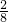 ,即
,即
所以阴影部分的面积是6×
 =1.5(平方厘米)
=1.5(平方厘米)答:阴影部分的面积是1.5平方厘米;
故答案为:1.5平方厘米
分析:如图,由折叠可知,△ACE的面积等于△ADE的面积,AD=AC=3厘米,BD=5-3=2(厘米),由于△ADE和△BDE等高,AD:BD=3:2,因此,△ADE的面积:△BDE的面积=3:2,又由于,△ACE的面积等于△ADE的面积,△BDE的面积是△ABC面积的
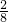 ,即
,即 ,△ABC的面积由题中提供数据即可求出,进而即可求出阴影部分(△BDE)面积.
,△ABC的面积由题中提供数据即可求出,进而即可求出阴影部分(△BDE)面积.点评:本题是考查图形的折叠问题、三角形面积的计算是等,此种解答方法的关键是理解△BDE的面积是△ABC面积的
 .此题还可用相似三角形解答.
.此题还可用相似三角形解答. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
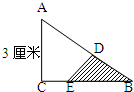 直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.
直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.
 下图中直角三角形ABC的面积81平方厘米,过三角形ABC内的P点作三条边的平行线,且AD:DE:EC=2:3:4.求图中阴影面积的和.
下图中直角三角形ABC的面积81平方厘米,过三角形ABC内的P点作三条边的平行线,且AD:DE:EC=2:3:4.求图中阴影面积的和.