题目内容
直角三角形ABC三条边分别是3厘米、4厘米、5厘米,如图所示,分别以三边为直径画半圆,求阴影部分面积.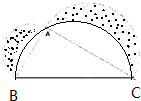

分析:以3厘米、4厘米和5厘米为直径画了三个半圆,其中以BC为半径的圆一定过A点,因为直角三角形ABC的∠A是直角,直径所对的角是直角;通过观察,发现:阴影部分的面积=半圆AB的面积+半圆AC的面积+三角形ABC的面积-半圆BC的面积,代入数值,即可得解.


解答:解:以AB为直径的圆半径=
AB=3÷2=1.5(厘米),此半圆的面积=
π×1.52=1.125π(平方厘米);
以AC为直径的圆半径=
AC=4÷2=2(厘米),此半圆的面积=
π×22=2π(平方厘米);
以BC为直径的圆半径=
BC=5÷2=2.5(厘米),此半圆的面积=
π×2.52=3.125π(平方厘米);
三角形ABC的面积=
AB?AC=3×4÷2=6(平方厘米);
所以阴影部分的面积=半圆AB的面积+半圆AC的面积+三角形ABC的面积-半圆BC的面积=1.125π+2π+6-3.125π=6(平方厘米);
答:阴影部分的面积是6平方厘米.
| 1 |
| 2 |
| 1 |
| 2 |
以AC为直径的圆半径=
| 1 |
| 2 |
| 1 |
| 2 |
以BC为直径的圆半径=
| 1 |
| 2 |
| 1 |
| 2 |
三角形ABC的面积=
| 1 |
| 2 |
所以阴影部分的面积=半圆AB的面积+半圆AC的面积+三角形ABC的面积-半圆BC的面积=1.125π+2π+6-3.125π=6(平方厘米);
答:阴影部分的面积是6平方厘米.
点评:此题考查了组合图形的面积,关键是看出:阴影部分面积=两个直角边上的半圆面积+三角形ABC的面积-斜边上半圆的面积,巧妙的是结果正好是直角三角形ABC的面积.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
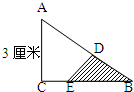 直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.
直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积. 下图中直角三角形ABC的面积81平方厘米,过三角形ABC内的P点作三条边的平行线,且AD:DE:EC=2:3:4.求图中阴影面积的和.
下图中直角三角形ABC的面积81平方厘米,过三角形ABC内的P点作三条边的平行线,且AD:DE:EC=2:3:4.求图中阴影面积的和.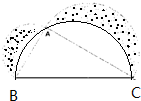
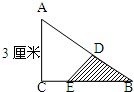 直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.
直角三角形ABC三条边长为3厘米、4厘米、5厘米,把AC对折到斜边AB上,AC与AD重合,如图,求阴影部分面积.