题目内容
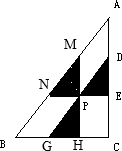
 下图中直角三角形ABC的面积81平方厘米,过三角形ABC内的P点作三条边的平行线,且AD:DE:EC=2:3:4.求图中阴影面积的和.
下图中直角三角形ABC的面积81平方厘米,过三角形ABC内的P点作三条边的平行线,且AD:DE:EC=2:3:4.求图中阴影面积的和.分析:观察图形,NE∥BC,所以∠DPE=∠PGH,∠DEP=∠C;又因为DG∥AB,所以∠PGH=∠B,所以∠DPE=∠B,由此可得三角形DPE与三角形ABC相似,相似比是DE:AC=3:(2+3+4)=1:3,因为相似三角形的面积之比等于相似比的平方,所以它们的面积之比是1:9,已知三角形ABC的面积是81平方厘米,所以三角形DPE的面积是:81÷9=9平方厘米,同理可以退出三角形DPE和三角形MNP、和三角形PGH相似,利用平行新发现的定理即可求出它们的相似比,再根据相似三角形的面积之比等于相似比的平方,即可求出三角形MNP和三角形PGH的面积,最后把三个三角形的面积加起来即可得出阴影部分的面积.

解答:解:NE∥BC,所以∠DPE=∠PGH,∠DEP=∠C;
又因为DG∥AB,所以∠PGH=∠B,所以∠DPE=∠B,
由此可得三角形DPE与三角形ABC相似,因为AD:DE:EC=2:3:4.
所以它们的相似比是DE:AC=3:(2+3+4)=1:3,则三角形DPE与三角形ABC的面积之比是1:9,
所以三角形DPE的面积是:81÷9=9(平方厘米),
同理,不难推出三角形DPE和三角形MNP、,相似比是:PE:NP=DE:AD=3:2;
所以面积之比是9:4,所以三角形MNP的面积是:9÷9×4=4(平方厘米),
同理,三角形DPE和三角形PGH也相似,相似比是:DP:PG=DE:EC=3:4,
所以三角形PGH的面积是9÷3×4=12(平方厘米),
9+4+12=25(平方厘米厘),
答:阴影部分的三角形的面积之和是25平方厘米.
又因为DG∥AB,所以∠PGH=∠B,所以∠DPE=∠B,
由此可得三角形DPE与三角形ABC相似,因为AD:DE:EC=2:3:4.
所以它们的相似比是DE:AC=3:(2+3+4)=1:3,则三角形DPE与三角形ABC的面积之比是1:9,
所以三角形DPE的面积是:81÷9=9(平方厘米),
同理,不难推出三角形DPE和三角形MNP、,相似比是:PE:NP=DE:AD=3:2;
所以面积之比是9:4,所以三角形MNP的面积是:9÷9×4=4(平方厘米),
同理,三角形DPE和三角形PGH也相似,相似比是:DP:PG=DE:EC=3:4,
所以三角形PGH的面积是9÷3×4=12(平方厘米),
9+4+12=25(平方厘米厘),
答:阴影部分的三角形的面积之和是25平方厘米.
点评:此题主要考查平行线的性质,相似三角形的判定、相似三角形的面积之比等于相似比的平方的灵活应用.

练习册系列答案
相关题目



