Question

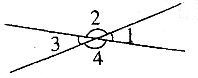
在如图中：∠1=30°，∠2=110°，∠3=（________）°，∠4=（________）°
我发现了：∠4=∠（________）+∠（________）

Answer 1

40    140    1    2
分析：观察图形可知，∠1、∠2、∠3在同一个三角形中，所以根据三角形的内角和是180°可得：∠3=180°-30°-110°=40°；又因为∠4与∠3组成了一个平角，所以∠4与∠3的和是180°，则∠4=180°-40°=140°；由此可得：∠4的度数等于∠1与∠2的和．
解答：根据题干分析可得：∠1+∠2=30°+110°=140°；
所以∠3=180°-140°=40°；
因为∠4与∠3组成了一个平角，
所以∠4=180°-40°=140°；
由上述计算可得：∠4=∠1+∠2．
故答案为：40；140；1；2．
点评：此题考查了三角形内角和定理的灵活应用以及三角形的一个外角等于和它不相邻的两个内角之和的推理方法．