题目内容
一个圆锥,增加后的高与原来的高的比是8:3.如果圆锥的体积不变,原来的底面积比现在的底面积大40cm2.现在的底面积是________cm2.
24
分析:设圆锥变化前后的体积相等为V,原来的高是3h,增加后的高是8h,根据圆锥的体积公式可得圆锥变化前后的底面积之比,由此即可解答.
解答:设圆锥变化前后的体积相等为V,原来的高是3h,增加后的高是8h,
则增加后的底面积与原来底面积之比是: :
: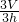 =3:8,
=3:8,
设现在的底面积是x平方厘米,则原来的底面积就是x+40,由此可得比例式:
x:(x+40)=3:8,
8x=3(x+40),
8x=3x+120,
5x=120,
x=24;
答:现在的底面积是24平方厘米.
故答案为:24.
点评:此题考查了圆锥的体积公式的灵活应用,关键是得出变化前后的两个圆锥的底面积之比.
分析:设圆锥变化前后的体积相等为V,原来的高是3h,增加后的高是8h,根据圆锥的体积公式可得圆锥变化前后的底面积之比,由此即可解答.
解答:设圆锥变化前后的体积相等为V,原来的高是3h,增加后的高是8h,
则增加后的底面积与原来底面积之比是:
 :
: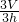 =3:8,
=3:8,设现在的底面积是x平方厘米,则原来的底面积就是x+40,由此可得比例式:
x:(x+40)=3:8,
8x=3(x+40),
8x=3x+120,
5x=120,
x=24;
答:现在的底面积是24平方厘米.
故答案为:24.
点评:此题考查了圆锥的体积公式的灵活应用,关键是得出变化前后的两个圆锥的底面积之比.

练习册系列答案
相关题目