题目内容
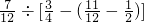
0.65×6.4-6.5×0.64+65×9%
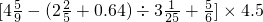
1-2+3-4+5-6+…+2009-2010+2011
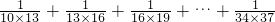
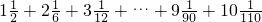 .
.
解:(1) ÷[
÷[ -(
-( -
- )],
)],
= ÷[
÷[ -
- ],
],
= ÷
÷ ,
,
= ×3,
×3,
= ;
;
(2)0.65×6.4-6.5×0.64+65×9%,
=0.65×6.4-6.5×0.64+65×0.09,
=0.65×6.4-0.65×6.4+0.65×9,
=0.65×(6.4-6.4+9),
=0.65×9,
=0.65×(10-1),
=6.5-0.65,
=5.85;
(3)[4 -(2
-(2 +0.64)÷3
+0.64)÷3 +
+ ]×4.5,
]×4.5,
=[4 -(2.4+0.64)÷3.04+
-(2.4+0.64)÷3.04+ ]×4.5,
]×4.5,
=[4 -3.04÷3.04+
-3.04÷3.04+ ]×4.5,
]×4.5,
=[4 -1+
-1+ ]×
]× ,
,
=[ +
+ ]×
]× ,
,
= ×
× +
+ ×
× ,
,
=16+3 ,
,
=19 ;
;
(4)1-2+3-4+5-6+…+2009-2010+2011,
=(2011-2010)+(2009-2008)+…+(7-6)+(5-4)+(3-2)+1,
=1+1+…+1,
=1×1005+1,
=1006;
(5) +
+ +
+ +…+
+…+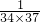 ,
,
= ×[(
×[( -
- )+(
)+( -
- )+(
)+( -
-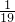 )+…+(
)+…+(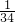 -
-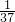 )],
)],
= ×[
×[ -
-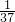 ],
],
= ×
×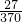 ,
,
=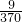 ;
;
(6)1 +2
+2 +3
+3 +…+9
+…+9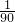 +10
+10 ,
,
=(1+2+3+…+9+10)+( +
+ +
+ +…+
+…+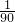 +
+ ),
),
=(1+10)×10÷2+(1- +
+ -
- +
+ -
- +…+
+…+ -
- +
+ -
- ),
),
=55+(1- ),
),
=55+ ,
,
=55 .
.
分析:(1)先算小括号内的,再算中括号内的,最后算括号外的;
(2)根据数字特点,原式变为0.65×6.4-0.65×6.4+0.65×9,运用乘法分配律简算;
(3)先算小括号内的,再算中括号内的除法,然后算中括号内的减法和减法,最后算括号外的乘法.同时注意数字转化;
(4)把此题调整一下运算顺序,从后向前,每两个数为一组,每一组结果为1,共分成(2011-1)÷2=1005组,最后剩余1,用1005加上1即可;
(5)通过观察,每个分数的分母中的两个数相差都是3,于是把原式变为 ×[(
×[( -
- )+(
)+( -
- )+(
)+( -
-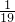 )+…+(
)+…+(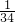 -
-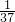 )],括号内通过分数加减相互抵消,求得结果;
)],括号内通过分数加减相互抵消,求得结果;
(6)把每个分数拆成整数+分数的形式,然后整数与整数相加,分数与分数相加.整数部分用高斯求和公式解答.分数部分中的每个分数又可以拆分成两个分数相减的形式,通过分数加减相互抵消,求得结果.
点评:考查了小数、分数的四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算.
 ÷[
÷[ -(
-( -
- )],
)],=
 ÷[
÷[ -
- ],
],=
 ÷
÷ ,
,=
 ×3,
×3,=
 ;
;(2)0.65×6.4-6.5×0.64+65×9%,
=0.65×6.4-6.5×0.64+65×0.09,
=0.65×6.4-0.65×6.4+0.65×9,
=0.65×(6.4-6.4+9),
=0.65×9,
=0.65×(10-1),
=6.5-0.65,
=5.85;
(3)[4
 -(2
-(2 +0.64)÷3
+0.64)÷3 +
+ ]×4.5,
]×4.5,=[4
 -(2.4+0.64)÷3.04+
-(2.4+0.64)÷3.04+ ]×4.5,
]×4.5,=[4
 -3.04÷3.04+
-3.04÷3.04+ ]×4.5,
]×4.5,=[4
 -1+
-1+ ]×
]× ,
,=[
 +
+ ]×
]× ,
,=
 ×
× +
+ ×
× ,
,=16+3
 ,
,=19
 ;
;(4)1-2+3-4+5-6+…+2009-2010+2011,
=(2011-2010)+(2009-2008)+…+(7-6)+(5-4)+(3-2)+1,
=1+1+…+1,
=1×1005+1,
=1006;
(5)
 +
+ +
+ +…+
+…+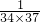 ,
,=
 ×[(
×[( -
- )+(
)+( -
- )+(
)+( -
-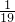 )+…+(
)+…+(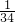 -
-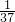 )],
)],=
 ×[
×[ -
-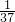 ],
],=
 ×
×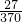 ,
,=
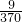 ;
;(6)1
 +2
+2 +3
+3 +…+9
+…+9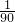 +10
+10 ,
,=(1+2+3+…+9+10)+(
 +
+ +
+ +…+
+…+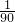 +
+ ),
),=(1+10)×10÷2+(1-
 +
+ -
- +
+ -
- +…+
+…+ -
- +
+ -
- ),
),=55+(1-
 ),
),=55+
 ,
,=55
 .
.分析:(1)先算小括号内的,再算中括号内的,最后算括号外的;
(2)根据数字特点,原式变为0.65×6.4-0.65×6.4+0.65×9,运用乘法分配律简算;
(3)先算小括号内的,再算中括号内的除法,然后算中括号内的减法和减法,最后算括号外的乘法.同时注意数字转化;
(4)把此题调整一下运算顺序,从后向前,每两个数为一组,每一组结果为1,共分成(2011-1)÷2=1005组,最后剩余1,用1005加上1即可;
(5)通过观察,每个分数的分母中的两个数相差都是3,于是把原式变为
 ×[(
×[( -
- )+(
)+( -
- )+(
)+( -
-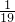 )+…+(
)+…+(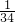 -
-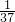 )],括号内通过分数加减相互抵消,求得结果;
)],括号内通过分数加减相互抵消,求得结果;(6)把每个分数拆成整数+分数的形式,然后整数与整数相加,分数与分数相加.整数部分用高斯求和公式解答.分数部分中的每个分数又可以拆分成两个分数相减的形式,通过分数加减相互抵消,求得结果.
点评:考查了小数、分数的四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
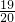 +
+ +
+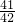 +
+ +
+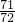 +
+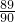 .
.