题目内容
 如图所示,在长方形ABCD中,放入6个形状、大小完全相同的长方形(长度如图,单位:厘米).图中阴影部分的面积是多少?
如图所示,在长方形ABCD中,放入6个形状、大小完全相同的长方形(长度如图,单位:厘米).图中阴影部分的面积是多少?分析:设小长方形的长是a,宽是b,如下图:
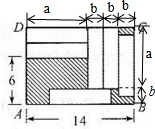
大长方形的长是a+3b,也就是14;
大长方形的宽是a+b,也就是6+2b;
由此列出两个等式,通过代换求出a和b的值;再根据阴影部分的面积=长方形ABCD的面积-6个小长方形的面积,利用长方形的面积公式表示出阴影部分的面积即可.

大长方形的长是a+3b,也就是14;
大长方形的宽是a+b,也就是6+2b;
由此列出两个等式,通过代换求出a和b的值;再根据阴影部分的面积=长方形ABCD的面积-6个小长方形的面积,利用长方形的面积公式表示出阴影部分的面积即可.
解答:解:设小长方形的长是a,宽是b,那么:
a+3b=14,①
a+b=6+2b,②
由②可得:
a-b=6;③
由①-③可得:
4b=8,
b=2;
把b=2代入③可得:
a-2=6,
a=8;
小长方形的长是8厘米,宽是2厘米;
大长方形的长是14厘米;宽是8+2=10(厘米);
图中阴影部分的面积是:
14×10-8×2×6,
=140-96,
=44(平方厘米);
答:图中阴影部分的面积是44平方厘米.
a+3b=14,①
a+b=6+2b,②
由②可得:
a-b=6;③
由①-③可得:
4b=8,
b=2;
把b=2代入③可得:
a-2=6,
a=8;
小长方形的长是8厘米,宽是2厘米;
大长方形的长是14厘米;宽是8+2=10(厘米);
图中阴影部分的面积是:
14×10-8×2×6,
=140-96,
=44(平方厘米);
答:图中阴影部分的面积是44平方厘米.
点评:此题是一个信息题目,要求学生会根据图示找出数量关系,然后利用数量关系等式,代换求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
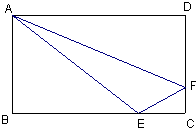 如图所示,在长方形ABCD中,△ABE、△ADF和四边形AECF的面积都相等,且BE=8,则EC的长为( )
如图所示,在长方形ABCD中,△ABE、△ADF和四边形AECF的面积都相等,且BE=8,则EC的长为( ) (2010?保靖县)如图所示,在相距10厘米的两条平行线d和c之间,有正方形A和长方形B.正方形A沿直线d以每秒2厘米的速度向右运动,长方形B固定不动,A和B两个图形有重叠部分的时间持续多少秒?(单位:厘米)
(2010?保靖县)如图所示,在相距10厘米的两条平行线d和c之间,有正方形A和长方形B.正方形A沿直线d以每秒2厘米的速度向右运动,长方形B固定不动,A和B两个图形有重叠部分的时间持续多少秒?(单位:厘米) 如图所示,在长方形ABCD中,AB=3,AC=5,从图中所示的位置开始,长方形在EF上不滑动地连续转两次,每次转动90°(虚线表示长方形转动后的位置),则顶点A经过的痕迹的长度是
如图所示,在长方形ABCD中,AB=3,AC=5,从图中所示的位置开始,长方形在EF上不滑动地连续转两次,每次转动90°(虚线表示长方形转动后的位置),则顶点A经过的痕迹的长度是 如图所示,在长方形内截取一个最大的正方形,阴影部分为剩余部分.剩余部
如图所示,在长方形内截取一个最大的正方形,阴影部分为剩余部分.剩余部 如图所示,在长方形ABCD中,AB=3,AC=5,从图中所示的位置开始,长方形在EF上不滑动地连续转两次,每次转动90°(虚线表示长方形转动后的位置),则顶点A经过的痕迹的长度是________(结果保留π).
如图所示,在长方形ABCD中,AB=3,AC=5,从图中所示的位置开始,长方形在EF上不滑动地连续转两次,每次转动90°(虚线表示长方形转动后的位置),则顶点A经过的痕迹的长度是________(结果保留π).