题目内容
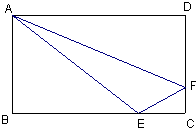如图所示，在长方形ABCD中，△ABE、△ADF和四边形AECF的面积都相等，且BE=8，则EC的长为（ ）分析：连接AC，根据长方形的对角线的特点可得：△ABC和△ADC的面积相等，是这个长方形面积的一半；又因为，△ABE、△ADF和四边形AECF的面积都相等，所以可得：△AEC的面积是四边形AECF的面积的一半，也是△ABE的一半，即：△ABE的面积：△ACE的面积=2：1，利用高一定时，三角形的面积与底成正比的性质即可得出BE：EC=2：1，由此即可求得EC的长度．
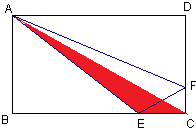
解答：解：连接AC，根据题干分析可得：
△ABE的面积：△ACE的面积=2：1，
所以：BE：EC=2：1，
又因为BE=8厘米，
所以EC=8÷2=4（厘米）；
故选：C．
△ABE的面积：△ACE的面积=2：1，
所以：BE：EC=2：1，
又因为BE=8厘米，
所以EC=8÷2=4（厘米）；
故选：C．
点评：此题连接AC，利用长方形的对角线的性质得出△ABE的面积与△ACE的面积的比，是解决本题的关键，然后利用高一定时，三角形面积与底成正比的关系即可解决问题．
练习册系列答案
相关题目
（2010?保靖县）如图所示，在相距10厘米的两条平行线d和c之间，有正方形A和长方形B．正方形A沿直线d以每秒2厘米的速度向右运动，长方形B固定不动，A和B两个图形有重叠部分的时间持续多少秒？（单位：厘米）
如图所示，在长方形ABCD中，AB=3，AC=5，从图中所示的位置开始，长方形在EF上不滑动地连续转两次，每次转动90°（虚线表示长方形转动后的位置），则顶点A经过的痕迹的长度是
如图所示，在长方形内截取一个最大的正方形，阴影部分为剩余部分．剩余部
如图所示，在长方形ABCD中，AB=3，AC=5，从图中所示的位置开始，长方形在EF上不滑动地连续转两次，每次转动90°（虚线表示长方形转动后的位置），则顶点A经过的痕迹的长度是________（结果保留π）．